Introduction to Random Signals and Noise

Appendix A

Representation of Signals in a Signal Space

A.1 LINEAR VECTOR SPACES

In order to facilitate the geometrical representation of signals, we treat them as vectors. Indeed, signals can be considered to behave like vectors, as will be shown in the sequel. For that purpose we recall the properties of linear vector spaces. A vector space is called a linear vector space if it satisfies the following conditions:

where x and y are arbitrary vectors and α and β are scalars.

In an n-dimensional linear vector space we define a so-called inner product as

where x_i and y_i are the elements of x and y, respectively. Two vectors x and y are said to be orthogonal if x · y = 0. The norm of a vector x is denoted by || x || and we define it by

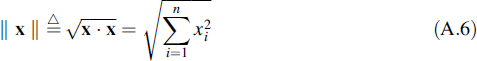
This norm has the following properties:

In general, we can state that the norm of a vector represents the distance from an arbitrary point described by the vector to the origin, or alternatively it is interpreted as the length of the vector. From Equation (A.9) we can readily derive the Schwarz inequality

A.2 THE SIGNAL SPACE CONCEPT

In this section we ...