Markov Chains: Analytic and Monte Carlo Computations

Solutions for the exercises

Solutions for Chapter 1

1. 1.1 This constitutes a Markov chain on 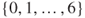with matrix
   
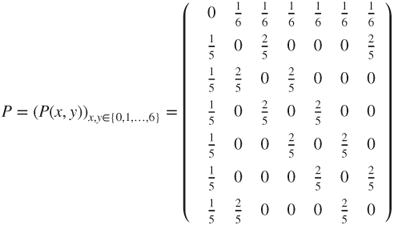
2. from which the graph is readily deduced. The astronaut can reach any module from any module in a finite number of steps, and hence, the chain is irreducible, and as the state space is finite, this yields that there exists a unique invariant measure 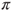. Moreover, 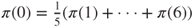and by uniqueness and symmetry, 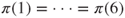, and hence, 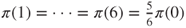. By normalization, we conclude that 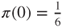and .
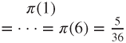3. 1.2 This constitutes a Markov chain on 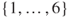with matrix
4. from which the graph is readily deduced. The mouse can reach one room from any other room ...