CHAPTER 7
Vector Spaces
In this chapter we introduce the concept of vector spaces. At the end of the chapter we introduce principal component analysis and explore its application to risk management.
VECTORS REVISITED
In the previous chapter we stated that matrices with a single column could be referred to as vectors. While not necessary, it is often convenient to represent vectors graphically. For example, the elements of a 2 × 1 matrix can be thought of as representing a point or a vector in two dimensions,1 as shown in Figure 7.1.
(7.1) ![]()
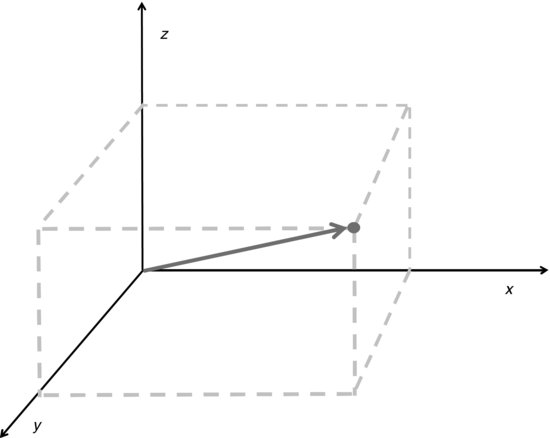
Similarly, a 3 × 1 matrix can be thought of as representing a point or vector in three dimensions, as shown in Figure 7.2.
(7.2) 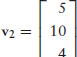
FIGURE 7.1 Two-Dimensional Vector
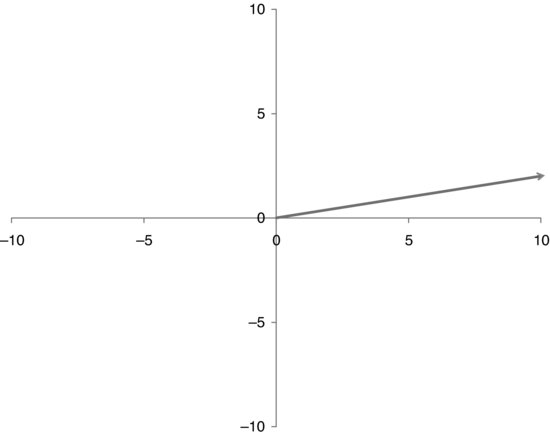
FIGURE 7.2 Three-Dimensional Vector
While it is difficult to visualize a point in higher dimensions, we can still speak of an n × 1 vector as representing a point or vector in n dimensions, for any positive value of n.
In addition to the operations of addition and scalar multiplication that we explored in the previous chapter, with vectors we can also compute the Euclidean inner product, ...

