Modeling, Estimation and Optimal Filtration in Signal Processing

Appendix E

Influence of an Additive White Noise on the Estimation of AR Parameters

Let y(k) be a p^th-order autoregressive process disturbed by an additive noise b(k) which is independent of the driving process u(k) i.e.:

In Chapter 2, we saw that the noisy observation z(k) can itself be considered as a p^th-order autoregressive process. In fact, we can easily show that:

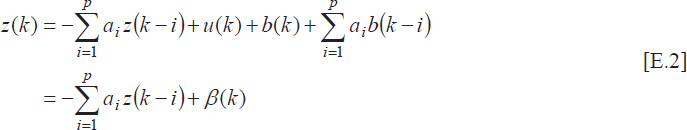
To understand and analyze the influence of the noise on the estimation of the AR parameters, Kay proposes a comparison between the spectral flatness ξ_y of the process y(k) and that of the observation z{k), i.e. ξ_z [1]. For any process x, the spectral flatness is defined as follows:

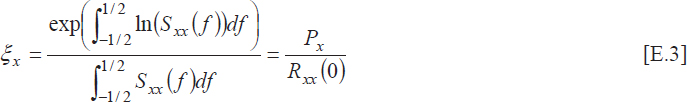
where S_xx(ω) and R_xx(τ) denote, respectively, the power spectral density and the autocorrelation function of the process.

When x(k) is an autoregressive process, it can be seen as a sequence w(k) filtered by a filter whose transfer function is H(z) = 1/ A(z). Since the poles of H(z) necessarily lie inside the unit circle in the z-plane, the filter with transfer function A(z) satisfies the following criterion⁴:

This implies that:

However, ...