6.5 Intrinsic Variability Identification
This section is devoted to identifying the full variability or uncertainty of model inputs, reviewing the main existing algorithms and the important research challenges remaining.
6.5.1 A General Formulation
The inverse problem thus leads to the following program:
(6.164) 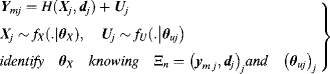
Note that realisations of x are deliberately assumed to be changing physically from the j-th to the j + 1-th experiment, taking the form of i.i.d. random variables Xj following the fixed distribution fX. Think, for instance, of mechanical observations of different pieces following a given design, but manufactured with (unavoidably) slightly varying dimensions. Thus, unlike traditional model calibration or data assimilation techniques, the inverse probabilistic algorithms considered hereafter do not foster the estimation of one fixed (although unknown) input value x explaining the data sample. They will process the information represented by Ξn in order to retrieve the parameters θX of the input uncertainty distribution fX.
Recall that in the general case, Maximal Likelihood Estimation (MLE) consists of maximising Equation 6.165 through the adjustment of some or all components of the vector θX (and/or of θuj):
Note that such an estimation program involves i.non-i.d. ...
Get Modelling Under Risk and Uncertainty: An Introduction to Statistical, Phenomenological and Computational Methods now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

