Optical Sources, Detectors, and Systems

2.2 Absorption or Amplification of Optical Waves 3 5

with B22 and

B22

the proportionality constants for the upward and

downward induced or stimulated transitions. Manipulation of the

second and fourth terms of

Eq.

(2.1) yields

(2.2)

N2

But we know from

Eq.

(1.12) that

8nhv^

"^ >(£"-/«-I)

and, therefore, to satisfy the relationship of Eq. (2.1) for all frequencies

and all temperatures,

8^2

= ^23 ~ ^/ ^^^ ^/^ -

Snhx^lc^-

Since we have

established that the upward and downward induced rates are equal, we

shall use the single constant

B,

which can be written

g^

^^ ^ ^ ^ ^ (2 3)

where

t^

is defined as the

spontaneous

emission time and is equal to J/A.

The actual values of the A and B coefficients are determined by the

specific system considered. Obviously the larger the thermal equilib-

rium absorption, as determined by the B coefficient, the smaller the

radiative or spontaneous emission time. Also, the higher the optical fre-

quency, the shorter is t^ for the same value of B or absorption

coef-

ficient.

2.2 Absorption or Amplification of Optical Waves

Since we are interested in the absorption or emission of a single-fre-

quency or

monochromatic

plane wave , we now propagate such a wave

as shown in Figure

2.2.

We assume that the intensity is small enough so

that it does not disturb the state populations and that the frequency of

the wave is v, which is at or near the "resonant" or characteristic fre-

36

Chapter 2 Interaction of Radiation with Matter

f:

'-'-..

%^:

)

/

Figure 2.2 Blackbody chamber with added plane wave of intensity /. The small numerals

represent particles in the upper, 2, or lower, 7, state.

quency of the transition, which we now call v^. Now as the wave prop-

agates it will induce upward and downward transitions and a con-

comitant decrease or increase in photons, if we imagine a thin slab of

area A and thickness dz the incident power, P = lA, will increase by

dilA) = Ad/, as shown in the figure. Then d? = Adl = dUjdi = V(du/dt) =

Adz(du/dt).

since the increase in power is equal to the added energy U

per unit time in the small volume.

dz

IF

P

+

dP

=

P

+

Adl

2.2 Absorption or Amplification of Optical Waves

37

Therefore,

f

=

f

= 7^

=

^[^^^'^^^^^^]''^^^^^^^^^"^^^"^

(2.4)

where n^ and ^2 are the number of particles per unit volume. The

bracketed quantity in the fourth term is the rate of increase in photons in

the volume. But this equation has the interesting problem that the

quantity u ^ the spectral energy density, is actually infinite since we are

talking about a monochromatic or single-frequency wave. We resolve this

dilemma by realizing that energy transitions are allowed over a small

range of frequencies about the center or resonant frequency v^. Thus

the effective spectral energy density u^ may then be written as w^ =

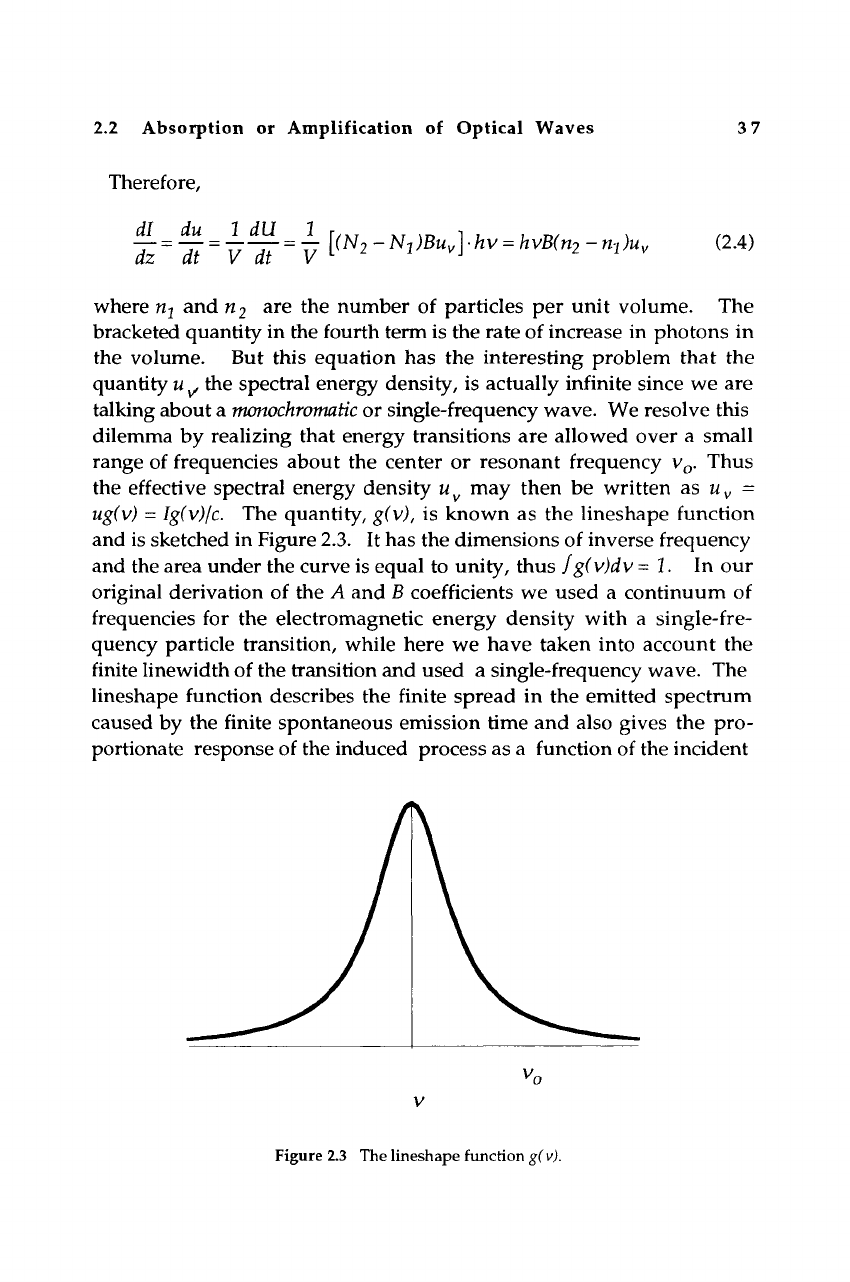
ugiv) = Ig(v)/c. The quantity, g(v), is known as the Uneshape function

and is sketched in Figure 2.3. It has the dimensions of inverse frequency

and the area under the curve is equal to unity, thus fg(v)dv

=

1. In our

original derivation of the A and B coefficients we used a continuum of

frequencies for the electromagnetic energy density with a single-fre-

quency particle transition, while here we have taken into account the

finite linewidth of the transition and used a single-frequency wave. The

Uneshape function describes the finite spread in the emitted spectrum

caused by the finite spontaneous emission time and also gives the pro-

portionate response of the induced process as a function of the incident

Figure 2.3 The lineshape function g(

v).