Optical Sources, Detectors, and Systems

126 Chapter 6 Heterodyne or Coherent Detection and Optical Amplification

(S/N)p = 1, becomes

(NEP)f^2T-

'^vB/rj.

This is one-half the value we

derived for direct or incoherent detection in the signal or photon-noise-

limited case. This may be understood if we realize that the if. signal

bandwidth, B, for any signal waveform is twice the bandwidth required

at baseband in direct detection, because of the upper and lower side-

bands about the center

i.f.

frequency in the heterodyne case. In general

a pulse envelope of width

T

at radio or optical frequencies produces a

signal with a bandwidth given by

B

=

2/T.

As we noted earlier, the the-

oretical heterodyne NEP may be achieved by sufficient local oscillator

power, such that the detection system is shot noise limited. Because the

i.f. power increases at the same rate as the noise j)Ower with increasing

iiQ, the noise of the amplifier stage can be made negligible.

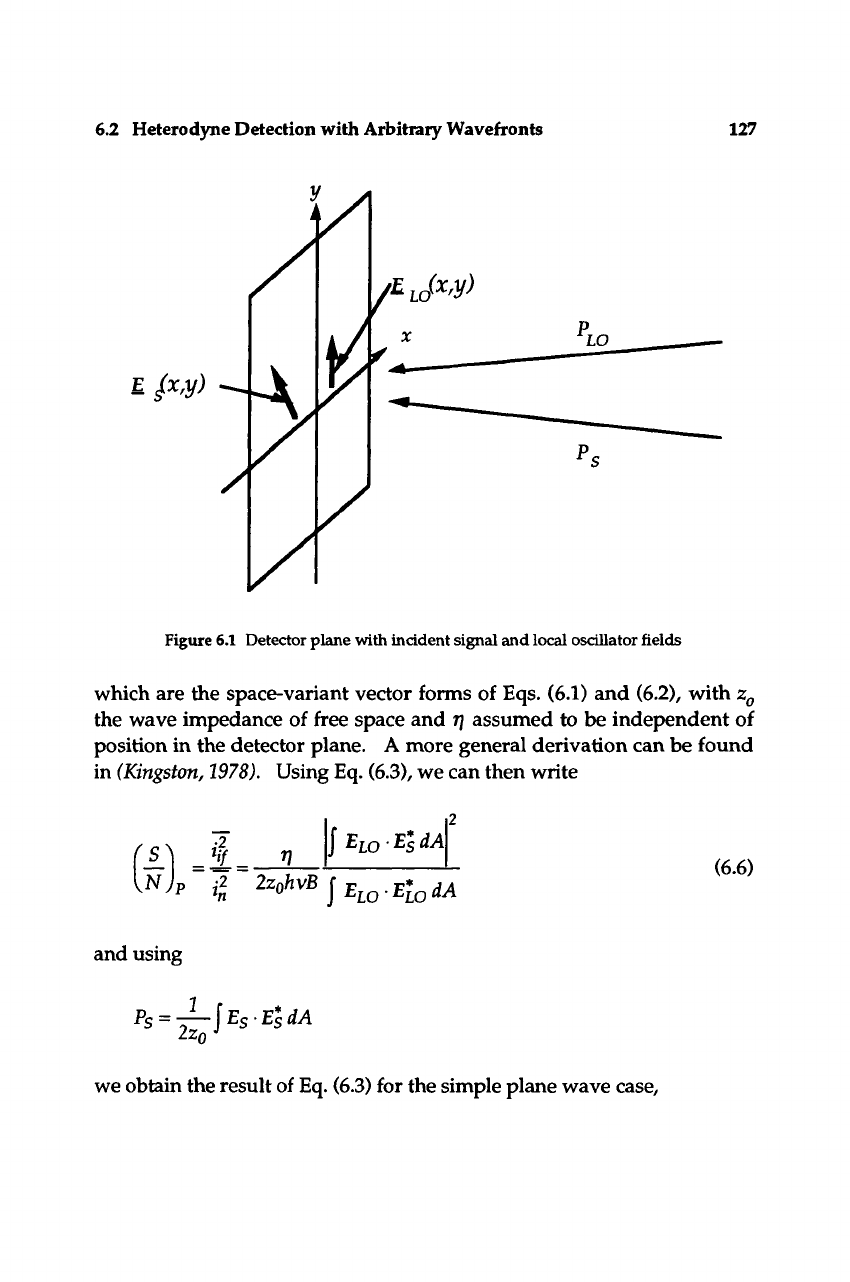
6.2 Heterodyne Detection with Arbitrary Wavefronts

Thus far, we have treated a uniform plane wave and have also

neglected the relative polarizations of the signal and local oscillator

waves. We now treat the general case, using the configuration of Figure

6.1,

with arbitrary waves producing electric fields on the detector plane

defined by

Es(x.y.t) = Rt[Es(x,y)eJ^st] ^^^^

ELo(^.y.t) = Rt[Eio(x,y)ei''^ot]

where the bold type indicates a spatial vector, and the fields

E(x,y)

are

complex. Using this formulation, we may write the signal, local

oscillator, and intermediate frequency currents as

6.2 Heterodyne Detection with Arbitrary Wavefronts 127

I S^fV)

Figure 6.1 Detector plane with incident signal and local oscillator fields

which are the space-variant vector forms of Eqs. (6.1) and (6.2), with z^

the wave impedance of free space and t] assumed to be independent of

position in the detector plane. A more general derivation can be found

in

(Kingston,

1978).

Using

Eq.

(6.3), we can then write

(6.6)

and using

2zn

we obtain the result of

Eq.

(6.3) for the simple plane wave case.