CHAPTER 7Rates‐Equity Hybrid Modelling

7.1 STATEMENT OF PROBLEM

Having derived the general form of multi‐factor pricing kernels in the preceding chapter, we look now to apply this knowledge first to a relatively simple problem, considering the joint distribution of equity and rates with a view to calculating a pricing kernel for rates‐equity hybrid derivatives. For rates we assume the short‐rate model of Hull and White [1990], as described in Chapter 4, using the notation there introduced. We suppose the equity process upper S Subscript t to be given by

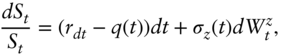
(7.1)StartFraction d upper S Subscript t Baseline Over upper S Subscript t Baseline EndFraction equals left-parenthesis r Subscript dt Baseline minus q left-parenthesis t right-parenthesis right-parenthesis dt plus sigma Subscript z Baseline left-parenthesis t right-parenthesis d upper W Subscript t Superscript z Baseline comma

with r Subscript d t given by (4.2), q left-parenthesis t right-parenthesis the dividend rate and upper W Subscript t Superscript z a Brownian motion. Further, take this Brownian motion to be correlated with that driving the Hull–White rates model, with

(7.2)corr left-parenthesis upper W Subscript t Baseline comma upper W Subscript t Superscript z Baseline right-parenthesis equals rho Subscript d z Baseline period

As previously, define an auxiliary process z Subscript t implicitly by (3.45). It follows ...

Get Perturbation Methods in Credit Derivatives now with the O’Reilly learning platform.

O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

Start your free trial