Primes of the Form x2+ny2: Fermat, Class Field Theory, and Complex Multiplication

CHAPTER ONE

FROM FERMAT TO GAUSS

§1. FERMAT, EULER AND QUADRATIC RECIPROCITY

In this section we will discuss primes of the form x² + ny², where n is a fixed positive integer. Our starting point will be the three theorems of Fermat for odd primes p

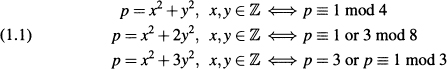
mentioned in the introduction. The goals of §1 are to prove (1.1) and, more importantly, to get a sense of what's involved in studying the equation p = x² + ny² when n > 0 is arbitrary. This last question was best answered by Euler, who spent 40 years proving Fermat's theorems and thinking about how they can be generalized. Our exposition will follow some of Euler's papers closely, both in the theorems proved and in the examples studied. We will see that Euler's strategy for proving (1.1) was one of the primary things that led him to discover quadratic reciprocity, and we will also discuss some of his remarkable conjectures concerning p = x² + ny² for n > 3. These conjectures touch on quadratic forms, composition, genus theory, cubic and biquadratic reciprocity, and will keep us busy for the rest of the chapter.

A. Fermat

Fermat's first mention of p = x² + y² occurs in a 1640 letter to Mersenne [35, Vol. II, p. 212], while p = x² + 2y² and p = x² + 3y² come later, first appearing in a 1654 letter to Pascal [35, Vol. II, pp. 310–314]. Although no proofs are given in these letters, Fermat states the results as theorems. Writing to Digby ...