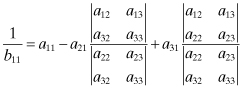Principles of Microelectromechanical Systems

APPENDIX

Consider the set of equations

(A.1)

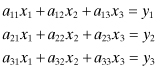
which can be expressed as

(A.2)

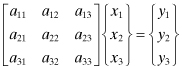
or

(A.3)

where

(A.4)

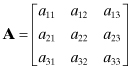
(A.5)

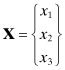
(A.6)

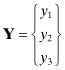
The solution is represented by

(A.7)

where

(A.8)

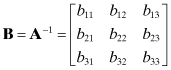
denotes the inverse matrix of A to be determined. We shall use Cramer’s rule to find the inverse matrix. Applying Cramer’s rule (Kreyszig, 1979) to (A.2), we have x₁:

(A.9)

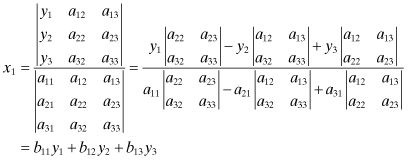
If we wish to find b_ij in terms of a_ij, b_ij may be expressed as

(A.10)

(A.11)

(A.12)

Similarly,

(A.13)

(A.14)

(A.15)

(A.16)

(A.17) ...