Principles of Solar Cells, LEDs and Related Devices, 2nd Edition

2 Derivation of the Uncertainty Principle

Consider a sinusoidal wave along the x ‐axis having amplitude a and wavelength λ . Its corresponding wave number k is defined as . We can express the wave as

If an electron is described by this wave it will have infinite spatial extent. A spatially localised wave packet may be obtained mathematically by adding a series of component sinusoidal waves together, each sinusoidal wave having a unique wavelength. This forms a Fourier series.

Consider the following sum of waves

This may be written as an integral in the case of a continuum of wavelengths:

A2.1

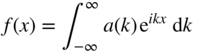
Assume, for simplicity, that only a range of wavelengths of the component waves exists such that

and outside of this range a(k) = 0.

Now we obtain

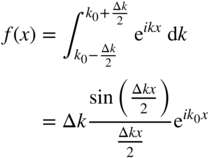
The amplitude of this wave is now in the form of a sinc function. We will approximate the width of the sinc function ...