8 Continuous System Vibration
Section 8.1: Continuous Systems
8.1. A transverse beam is supported by torsional springs at both ends with each spring having stiffness
k. Find the equation of motion and corresponding boundary conditions.
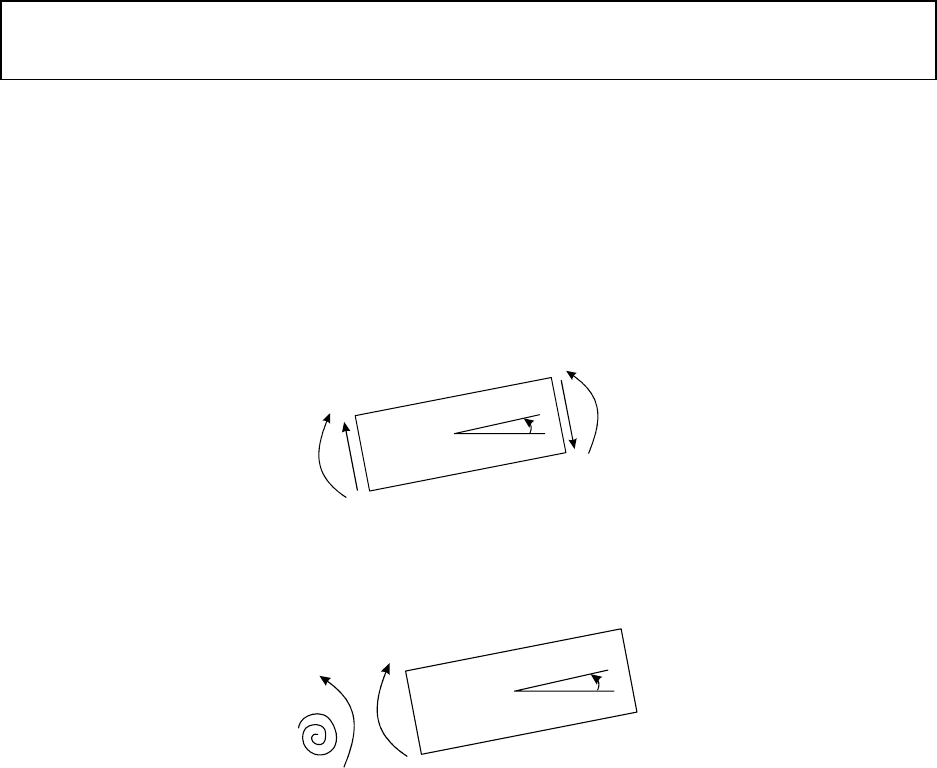
Solution: The boundary conditions are obtained by drawing a free body diagram. Let us define y be
positive upward and x be coordinate along the beam defined positive to the right. Then, the slope, moment,
and shear are given by
slope = y
moment = EIy
shear = (EIy
)
,
and defined positive as shown in Figure 29. Due to positive slope y
, the torsional spring on the left end
y'
M=EIy''
Q=(EIy'')'
Figure 29: Definition of positive slope, moment and shear.
y'
ky'
Figure 30: Moment due to torsional spring
exerts moment with magnitude ky
as shown in Figure 30. Then, we can write
EIy
(0, t) = ky
(0, t) .
Similarly, for the right end, we can write
EIy
(L, t) = −ky
(L, t) .
228
Section 8.2: Sturm-Liouville Eigenvalue Problem
8.2. A string is fixed at one end and is free to move up and down at the other end. Obtain the
eigenfunctions and eigenvalues.
Solution: The equation of motion and boundary conditions are given by
T y
−m¨y = 0 for 0 < x < L
y (0, t) = 0
y
(L, t) = 0.
Assuming y (x, t) = Y (X) f (t) , we can write
T Y
+ mω
2
Y = 0
Y (0) = 0
Y
(L) = 0.
The i
th
eigenfunction is given by
Y
i
= C
i
sin β
i
x,
where
β
i
L =
(2i − 1)
2
π
ω
i
= β
i
3
T
m
.
The eigenfunctions can be normalized with respect to m such that
L
0
mY
2
i
dx = 1
C
i
=
3
2
mL
.
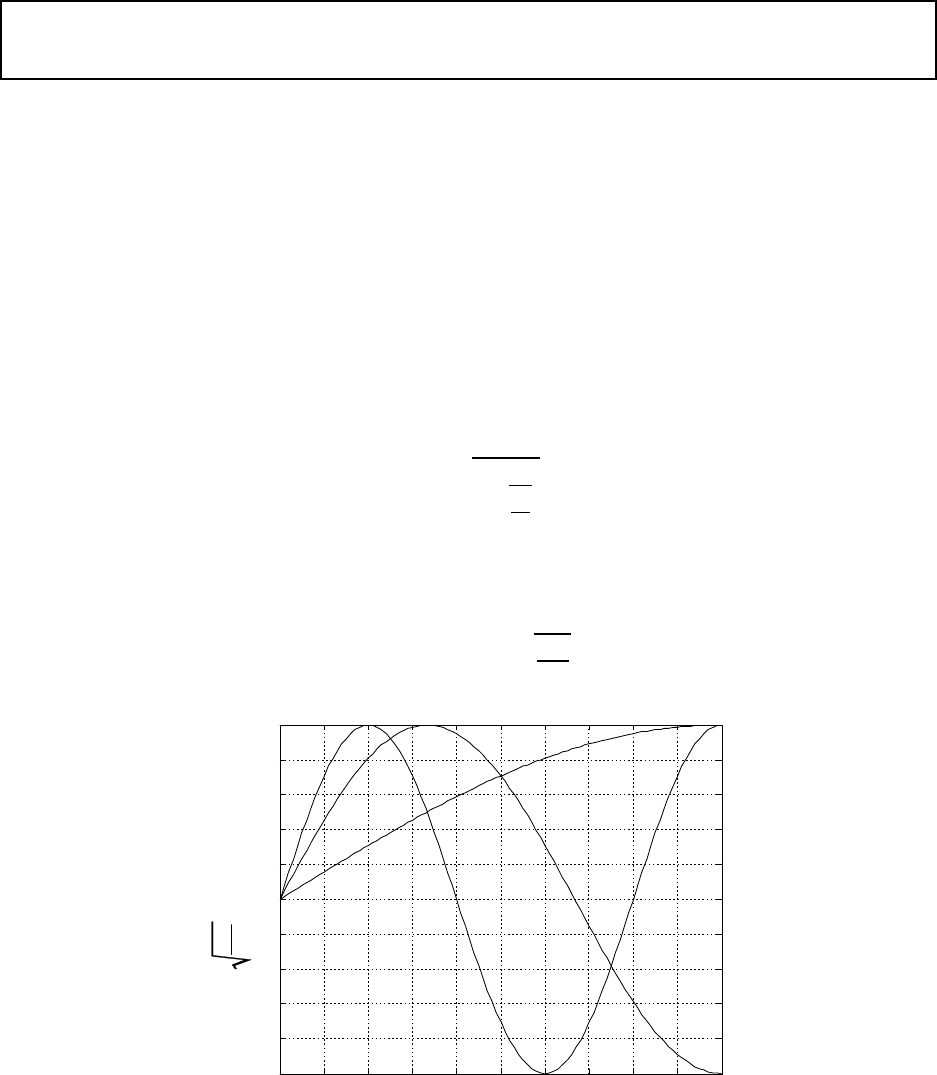
The figure below shows the first three mode shapes.
0 0.1 0.2 0.3 0.4
0.5
0.6
0.7
0.8
0.9
1
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
Y x
( )
x/L
i
= 1
i
= 2
i
= 3
m
L
2
i
Eigenfunctions for Problem 2. The first three mode shapes of a fixed-free string.
229

8.3. Prove the orthogonality condition for the string in Equation 8.12.
Solution: In the text, it was shown that
L
0
m (x) Y
n
(x)Y
r
(x)dx = δ
nr
.
Replacing m (x) Y
n
(x) by −T Y
n
(x) /ω
2
n
(spatial equation of motion) we can write
L
0
T Y
n
(x)Y
r
(x)dx = −ω
2
n
δ
nr
.
The left hand side can be integrated so that
T Y
n
(x) Y
r
(x) |
L
0
−
L
0
T Y
n
(x)Y
r
(x)dx = −ω
2
n
δ
nr
.
The term evaluated at the boundaries is reduced to zero, and we have
L
0
T Y
n
(x)Y
r
(x)dx = ω
2
n
δ
nr
.
230

8.4. Consider a uniform rod in axial vibration with mass per unit length m, length L, and axial stiffness
EA. The one end at x = 0 is attached to a spring with stiffness k and is free at x = L. Obtain the
eigenfunctions and eigenvalues. Use k = EA/L.
Solution: The spatial solution must satisfy
EAY
+ mω
2
Y = 0 for 0 < x < L
EAY
(0) − kY (0) = 0
Y
(L) = 0.
Then, the solution takes the form of
Y (x) = c
1
sin βx + c
2
cos βx,
where β =
m/EAω. From the first boundary condition, we obtain
c
2
=
EA
k
βc
1
.
From the second boundary condition, we obtain the characteristic equation given by
β cos βL −
EA
k
β
2
sin βL = 0.
If k = EA/L, the characteristic equation is reduced to
cos βL −βL sin βL = 0,
which yields
β
i
L = 0.86, 3.43, 6.44, ··· .
The corresponding eigenfunction is given by
Y
i
(x) = c
i
sin β
i
L
x
L
+ β
i
L cos β
i
L
x
L
.
Using the characteristic equation, this expression can be rewritten as
Y
i
(x) = d
i
cos
β
i
L
x
L
−1
,
where d
i
= c
i
/ sin β
i
L. The constant coefficient d
i
is determined by normalizing the eigenfunctions and is
given by
d
i
=
3
2
mL
1
1 + sin β
i
L
.
The next figure shows the first three eigenfunctions.
231
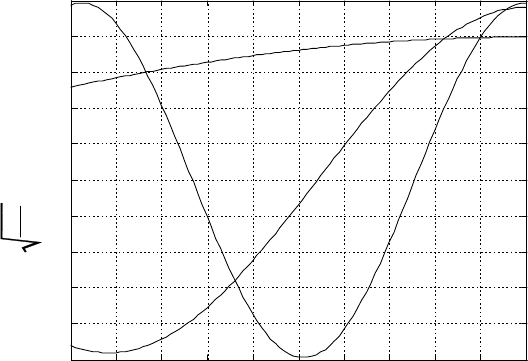
0 0.1 0.2 0.3 0.4
0.5
0.6
0.7
0.8
0.9
1
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
Y x
( )
x/L
i
= 1
i
= 2
i
= 3
m
L
2
i
Eigenfunctions for Problem 4.
232
Get Probabilistic Models for Dynamical Systems, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

