Probability and Statistics for Finance

Appendix A. Important Functions and Their Features

In this appendix, we review the functions that are used in some of the chapters in this book. In particular, we introduce the concept of continuous functions, the indicator function, the derivative of a function, monotonic functions, and the integral. Moreover, as special functions, we get to know the factorial, the gamma, beta, and Bessel functions as well as the characteristic function of random variables,

CONTINUOUS FUNCTION

In this section, we introduce general continuous functions.

General Idea

Let f(x) be a continuous function for some real-valued variable x. The general idea behind continuity is that the graph of f(x) does not exhibit gaps. In other words, f(x) can be thought of as being seamless. We illustrate this in Figure A.1. For increasing x, from x = 0 to x = 2, we can move along the graph of f(x) without ever having to jump. In the figure, the graph is generated by the two functions f(x) = x² for x∈[0,1) and f(x) = ln(x) + 1 for x∈[1,2).^[276]

A function f(x) is discontinuous if we have to jump when we move along the graph of the function. For example, consider the graph in Figure A.2. Approaching x = 1 from the left, we have to jump from f(x) = 1 to f(1) = 0. Thus, the function f is discontinuous at x = 1. Here, f is given by f(x)=x² for x∈[0,1) and f(x) = ln(x) for x∈[1,2).

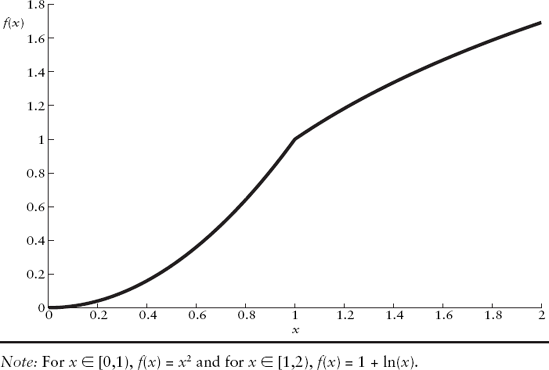
Figure A.1. Continuous Function f(x)

Figure A.2. Discontinuous ...