Probability and Statistics with Reliability, Queuing, and Computer Science Applications, 2nd Edition

Chapter 2Discrete Random Variables

2.1 Introduction

Thus far we have treated the sample space as the set of all possible outcomes of a random experiment. Some examples of sample spaces we have considered are

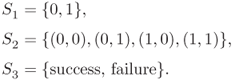
Some experiments yield sample spaces whose elements are numbers, but some other experiments do not yield numerically valued elements. For mathematical convenience, it is often desirable to associate one or more numbers (in addition to probabilities) with each possible outcome of an experiment. Such numbers might naturally correspond, for instance, to the cost of each experimental outcome, the total number of defective items in a batch, or the time to failure of a component.

Through the notion of random variables, this and the following chapter extend our earlier work to develop methods for the study of experiments whose outcomes may be described numerically. Besides this convenience, random variables also provide a more compact description of an experiment than the finest grain description of the sample space. For example, in the inspection of manufactured products, we may be interested only in the total number of defective items and not in the nature of the defects; in a sequence of Bernoulli trials, we may be interested only in the number of successes and not in the actual sequence of successes and failures. The notion of random variables provides us the power of abstraction ...