Probably Not, 2nd Edition

3Building a Bell

When a new random variable is created by summing other random variables, whether or not they all have the same probability distribution functions (PDFs), something special happens.

Rolling dice is an excellent example of this phenomenon. We know that there are six possible results for one die – the integers from 1 to 6. Since all six possible results are equally likely, the PDF of the rolling of a die is a uniform distribution with a probability of for each possible event.

Let's examine in detail what happens when we add up the results of several dice rolls. We can roll several dice or roll one die several times.

For the roll of one die one time, the PDF is simple, as shown in Figure 3.1.

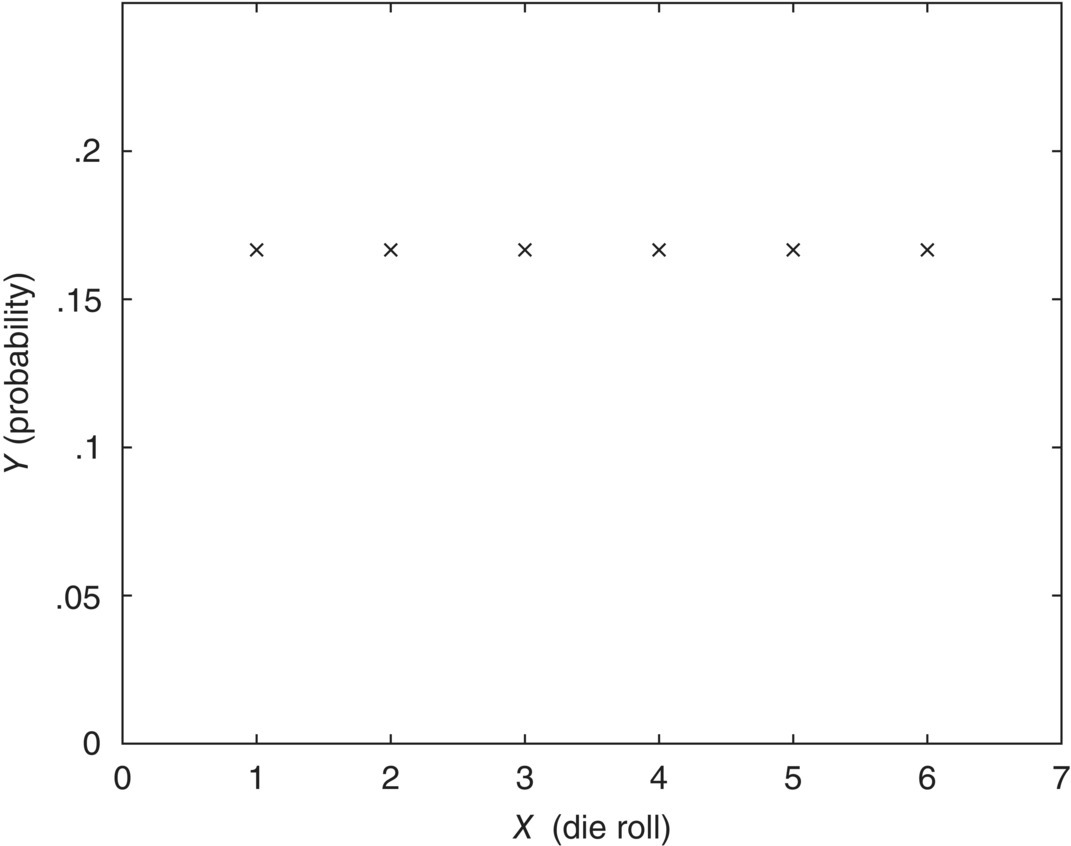
Figure 3.1 Uniform discrete PDF.

Now let's get a second die, identical to the first. Roll them both and consider the sum of the two individual results. Clearly, this sum must be a number between 2 and 12 (1 on both dice and 6 on both dice, respectively). Table 1.2 shows all the possible results.

There are – of course – 36 possible combinations of the two dice, each combination having a probability of 1/36. However, since the sum must be an integer between 2 and 12, i.e. there are only 11 possible results. Also, except for sums of 2 and 12, there are more than one way to get ...