9.3 Cofinal chains in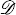 
9.3.1 Existence of a cofinal maximal chain of order type ω1
Definition 9.3.1. Given a partial ordering 〈P, <P〉, a set A ⊆ P is a cofinal chain if the members of A are linearly ordered under P and for any z ∈ P, there is an x ∈ A such that z ≤P x.
It is not difficult to see that under ZFC, there is a cofinal chain of Turing degrees if and only if CH holds. A natural question is whether there exists a cofinal maximal chain of order type ω1 in 〈, ≤〉 assuming ZFC + CH. The question is considered in this section.
The following fact ...
Get Recursion Theory now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
