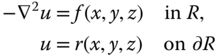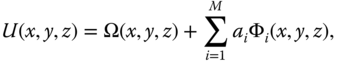Solving Partial Differential Equation Applications with PDE2D

Appendix BAlgorithms Used by PDE2D

This appendix includes frequent references to “The Numerical Solution of Ordinary and Partial Differential Equations, Third Edition” (Sewell 2015), and “Computational Methods of Linear Algebra, Third Edition” (Sewell 2014), where many of the algorithms used are described in more detail.

B.1 The Galerkin and Collocation Finite Element Methods

By far the most widely used form of the finite element method is the Galerkin method, and it is one of the two finite element variants used by PDE2D. We will illustrate its use for the following simple 3D steady‐state PDE and will discuss the time‐dependent and eigenvalue problems later, in Sections B.6 and B.7:

(B.1)

We try to find an approximate solution of the form

(B.2)

where is a set of linearly independent basis functions that vanish on the boundary and is another function that satisfies the boundary condition on . Clearly, will satisfy the boundary condition regardless of the values chosen for .