Solving Partial Differential Equation Applications with PDE2D

IIntroduction to PDE2D

I.1 The Collocation and Galerkin Finite Element Methods

PDE2D is a general‐purpose partial differential equation (PDE) solver that solves very general systems of nonlinear, steady‐state, time‐dependent, and eigenvalue PDEs in 1D intervals, general 2D regions (see Figure I.1), and a wide range of simple 3D regions (see Figure I.2), with general boundary conditions.

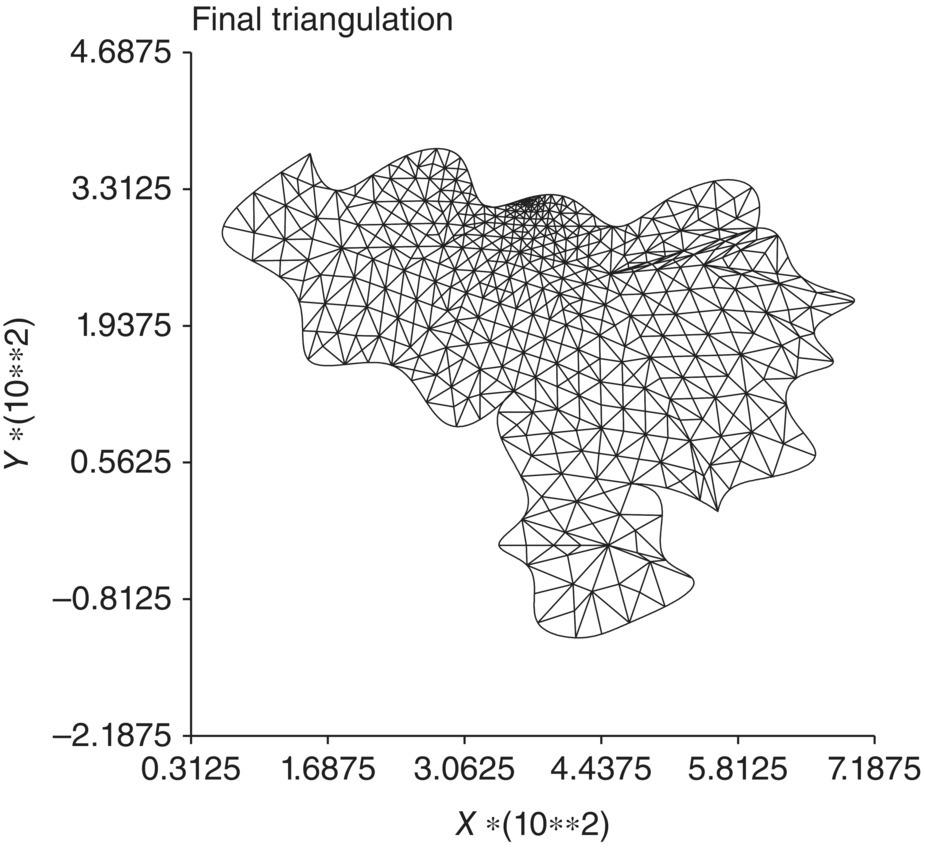
Figure I.1 Triangulation of Venezuela.

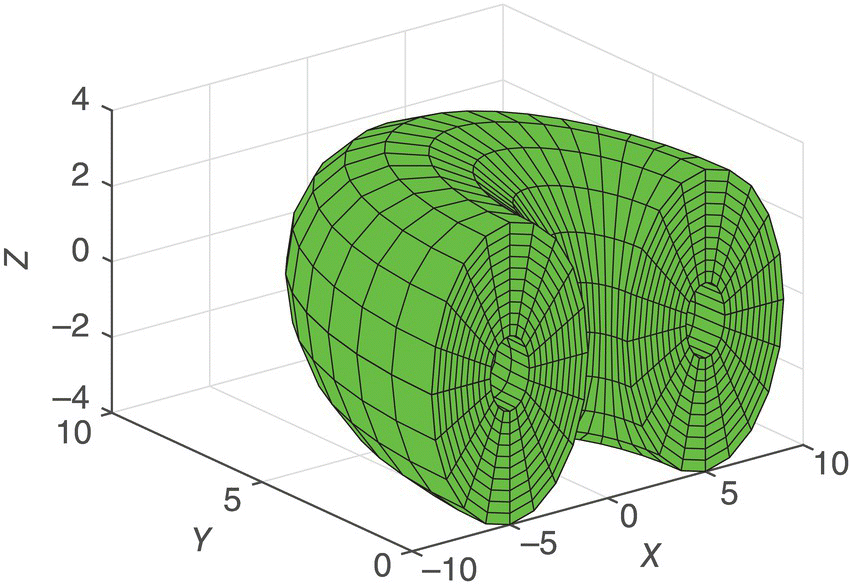
Figure I.2 3D grid, hollowed‐out half torus.

PDE2D uses a collocation finite element method for 3D problems, and either a collocation or Galerkin finite element method can be used for 1D and 2D problems. This book is primarily concerned with using PDE2D to solve applications, so we will not attempt in this section to explain the mathematics behind either method. Readers who want to know more about the mathematics should read Appendix B and for more details, The Numerical Solution of Ordinary and Partial Differential Equations (Third Edition) (Sewell 2015). Here we are only concerned with helping users decide which method to use.

There are two major differences between the collocation and Galerkin methods, as far as users are concerned:

1. The Galerkin method requires that PDEs be in “divergence” form. For 2D steady‐state problems, this means it must be ...