CHAPTER 2
PRELIMINARIES
Outline
2.5 Multivariate Normal Distribution
2.6 Multivariate t-Distribution
In this chapter, we discuss some basic results on various distributions, particularly the normal, chi-square, Student’s t-, multivariate t-distributions.
2.1 Normal Distribution
The most basic distribution in statistical theory is the normal distribution, ![]() (θ, σ2), with pdf
(θ, σ2), with pdf
(2.1.1) 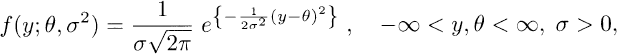
where θ is the mean and σ2 is the variance of this distribution.
It is well known that
(2.1.2) ![]()
(2.1.3) 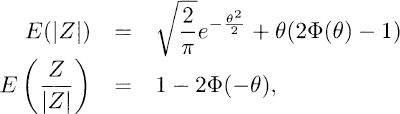
Get Statistical Inference for Models with Multivariate t-Distributed Errors now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

