CHAPTER 4
SIMPLE REGRESSION MODEL
Outline
4.2 Estimation and Testing of η
4.3 Properties of Intercept Parameter
In this chapter, we discuss some of the basic results from a simple regression model under the assumption that the error-vector is distributed according to the multivariate t-distribution. For normal errors see Saleh (2006) and for t-errors see Khan and Saleh (1997, 2008).
4.1 Introduction
Consider a simple linear model
where Y = (Y1, Y2, …, Yn)′ is the response vector and x = (x1, x2, …, xn)′ is a fixed vector of known constants, while ε = (ε1, ε2, …, εn)′ is the error vector distributed according to the low belonging to the class of multivariate t-distributions, say, M(n)t (0, σ2Vn, γo).
As in Chapter 3, the covariance matrix is formulated as
(4.1.2) 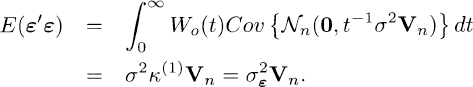
4.2 Estimation and Testing of η
In this section, we consider LSE of η and test of hypothesis, H0 : η = ηo vs HA : η ≠ ηo.
4.2.1 Estimation of η
For the LSE of η, we minimize
![]()
to obtain the LSE of η as
(4.2.1) 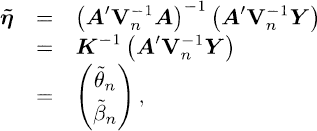
where
(4.2.2)
with K1 = 1′V−1n1, K
Get Statistical Inference for Models with Multivariate t-Distributed Errors now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

