Statistics for Process Control Engineers

5Probability Density Function

The probability density function (PDF) is a mathematical function that represents the distribution of a dataset. For example, if we were to throw a pair of unbiased six‐sided dice 36 times, we would expect (on average) the distribution of the total score to be that shown by Figure 5.1. This shows the frequency distribution. To convert it to a probability distribution we divide each frequency by the total number of throws. For example, a total score of 5 would be expected to occur four times in 36 throws and so has a probability of 4/36 (about 0.111 or 11.1%). Figure 5.2 shows the resulting probability distribution.

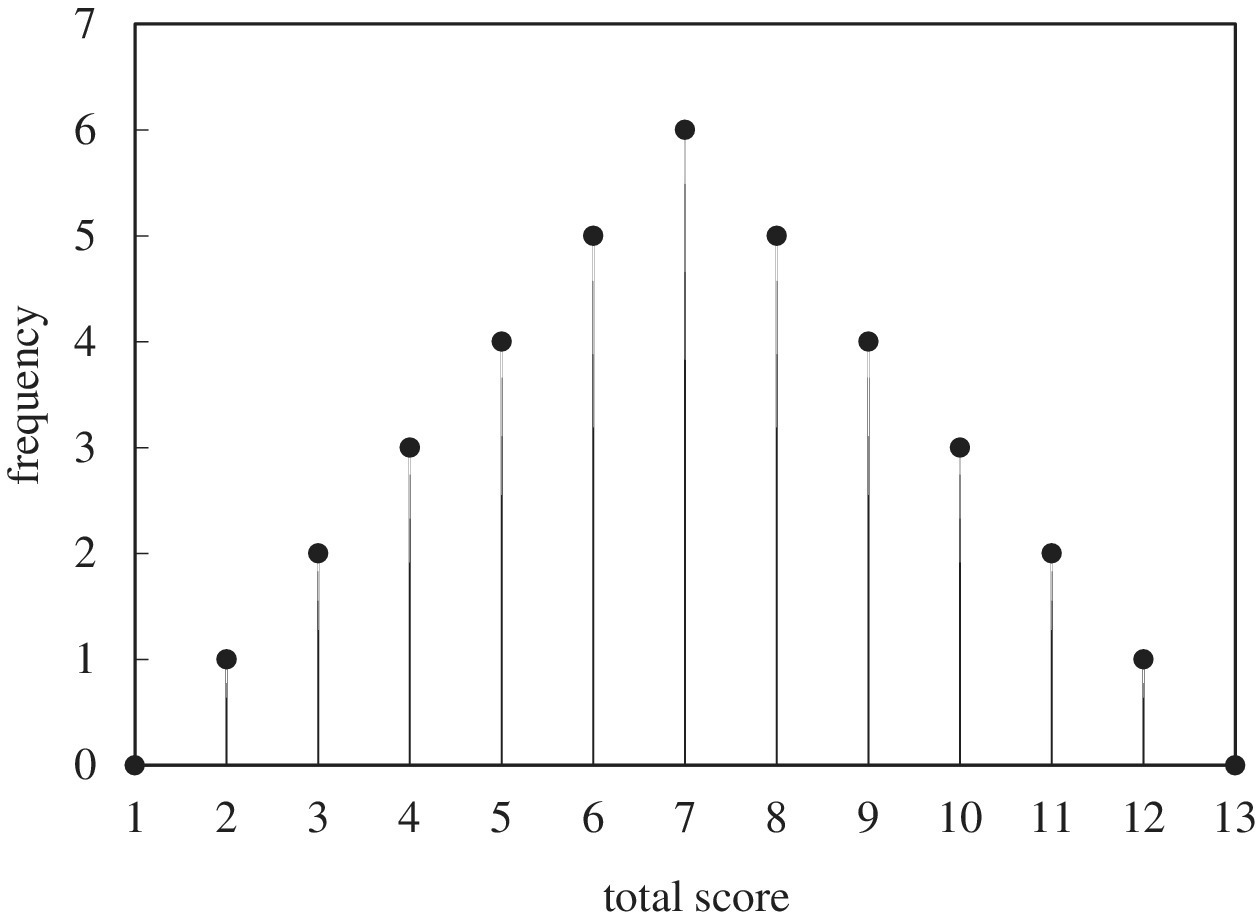
Figure 5.1 Expected frequency of total score from two dice

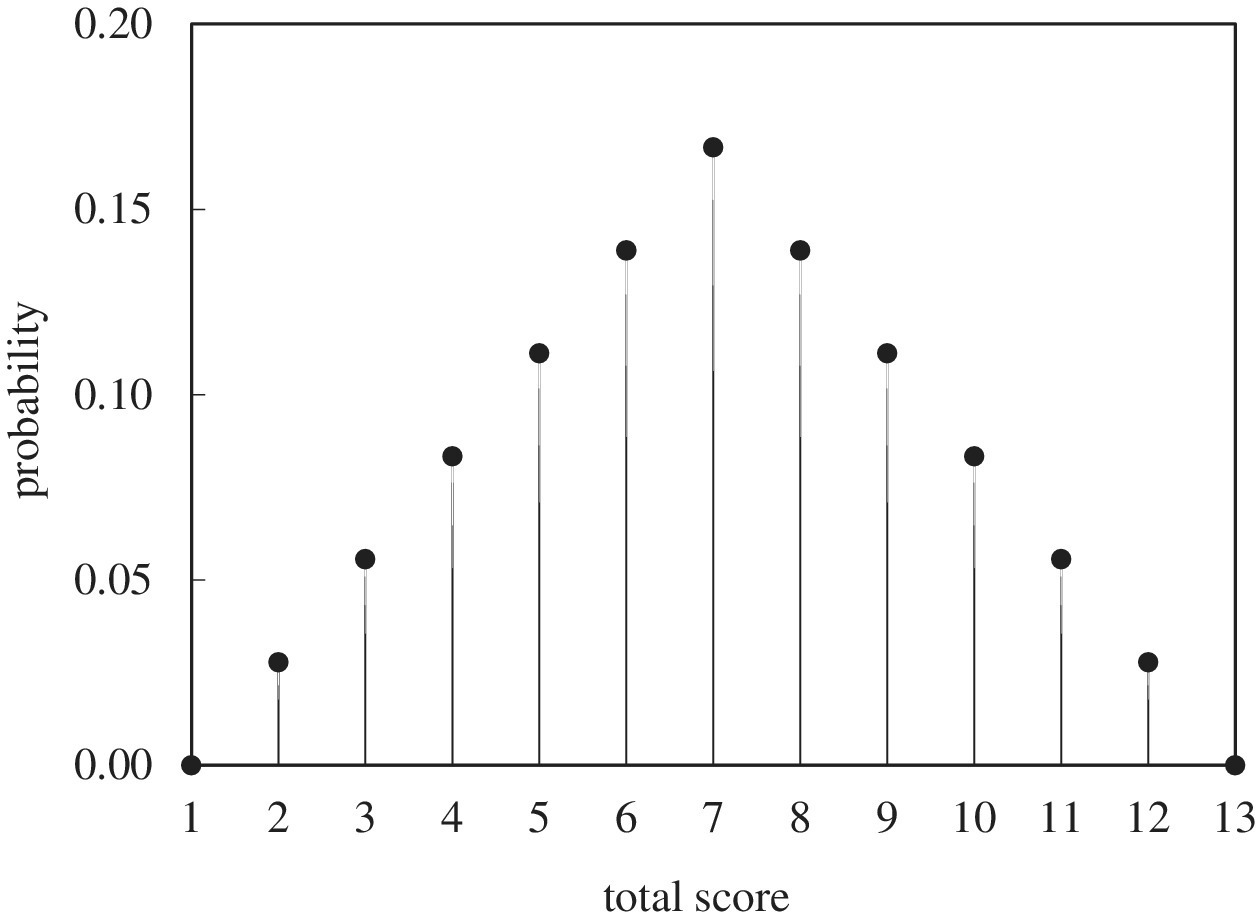
Figure 5.2 Expected distribution

Throwing dice generates a discrete distribution; in this case the result is restricted to integer values. Probability should not be plotted as continuous line. The probability of a non‐integer result is zero. But we can develop an equation for the line. In this case, if x is the total scored, the probability of scoring x is

(5.1)

Because x is discrete this function is known as the probability mass function (PMF). If the distribution were continuous ...