Statistics for Process Control Engineers

8Significance Testing

One of the key reasons we might want to fit a statistical distribution to process data is to explore whether an observed result is expected from normal process variations or whether it is exceptional. Significance testing enables us to establish whether our expectation of process variations is correct. Related to this, the confidence interval gives the range over which we might expect a process condition to vary.

8.1 Null Hypothesis

The probability (p) of an unbiased coin landing heads when tossed is 0.5. If we toss it 100 times we would expect it to land heads 50 times. We will show later how the binomial distribution is used to calculate the probability of this outcome but we should be quite surprised if it occurred since, as Figure 8.1 shows, the probability is only 8%. If it landed heads 49 times we would accept that this is just chance and would not doubt that the coin is unbiased. Clearly, if it landed heads 99 times, we would. The question is how many times must it land heads before we conclude that the coin is biased? For example, the probability of 60 heads is small at 0.011. Is this sufficiently low for us to conclude that p is actually closer to 0.6?

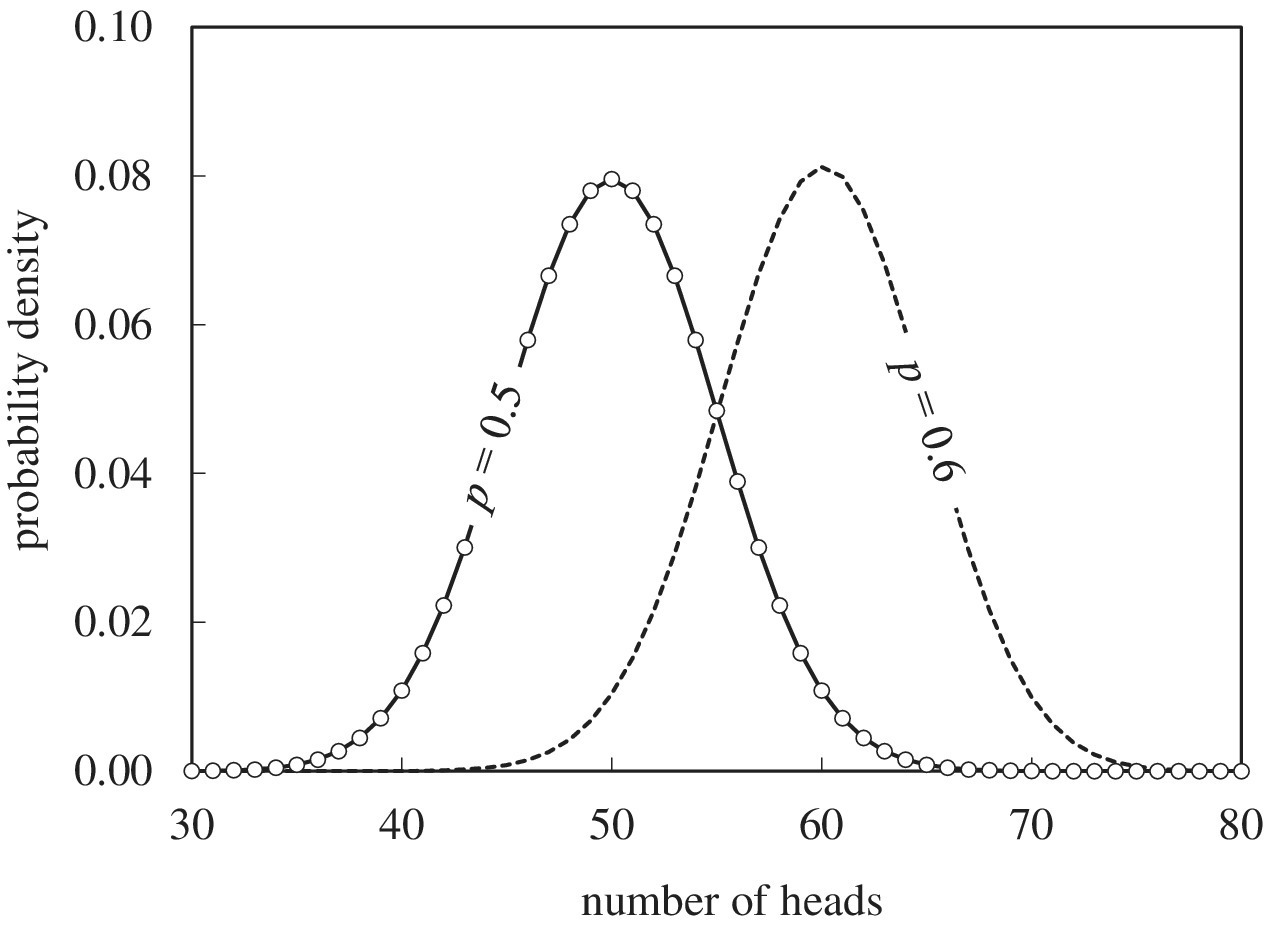
Figure 8.1 Probability density of the number of heads from 100 tosses

The approach is to first make the null hypothesis, sometimes given the symbol H₀. In this example this might be that the ...