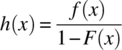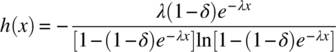Statistics for Process Control Engineers

14Hazard Function

The hazard function, sometimes described as the conditional failure density function or, more commonly, the failure rate is defined as

(14.1)

The reciprocal of the hazard function is known as the conditional failure density function.

Applying Equation (14.1) to the exponential distribution, described by Equations (12.61) and (12.62), gives

(14.2)

This tells us that the failure rate is constant at λ; it does not vary with time. The process has no memory.

Commonly the EL (exponential‐logarithmic) distribution is used. We will cover this in detail in Section 28.9. From Equations (28.33) and (28.34)

(14.3)

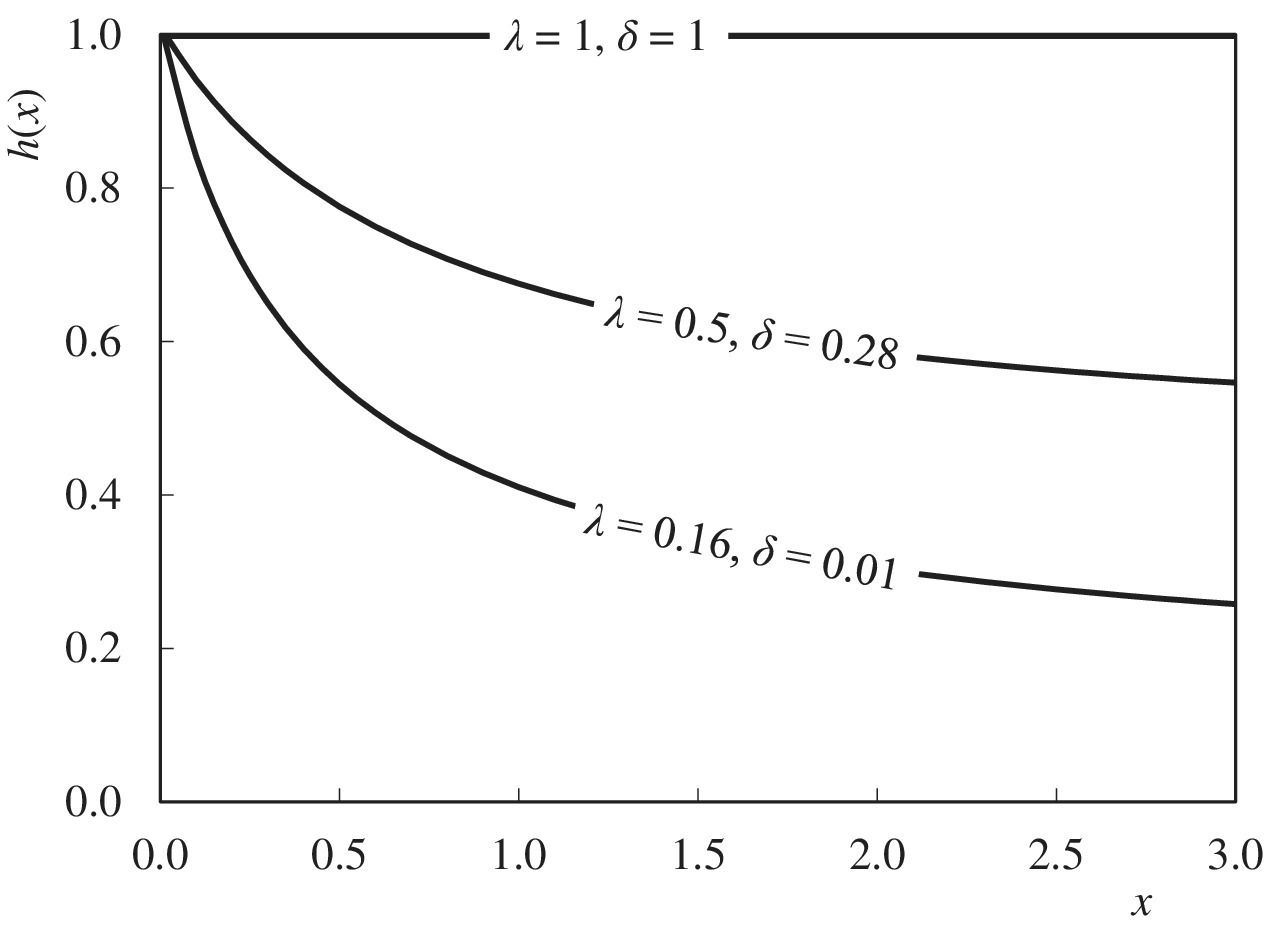
This function is plotted as Figure 14.1, with λ adjusted so that h(x) is 1 when x is zero. As δ → 1, Equation (14.3) becomes Equation (14.2). As δ is reduced below 1, the failure rate reduces over time. This might apply to the number of occasions a control scheme is disabled because of technical issues that are resolved over time. Or it may be because the operators initially did not properly understand its operation and this resolved by ongoing training.

Figure ...