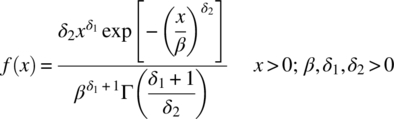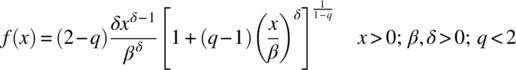Statistics for Process Control Engineers

29Weibull Distribution

We covered a number of the Weibull distributions in Section 12.8. Here we describe two enhanced versions.

29.1 Nukiyama–Tanasawa

The Nukiyama–Tanasawa distribution is an extension of the Weibull‐II distribution.

(29.1)

If δ₁ is set to δ₂ − 1, Equation (29.1) reverts to the Weibull‐II distribution, as shown by the coloured line in Figure 29.1. Varying δ₁ has an effect similar to that of δ₂. However, together they make the distribution a little more flexible.

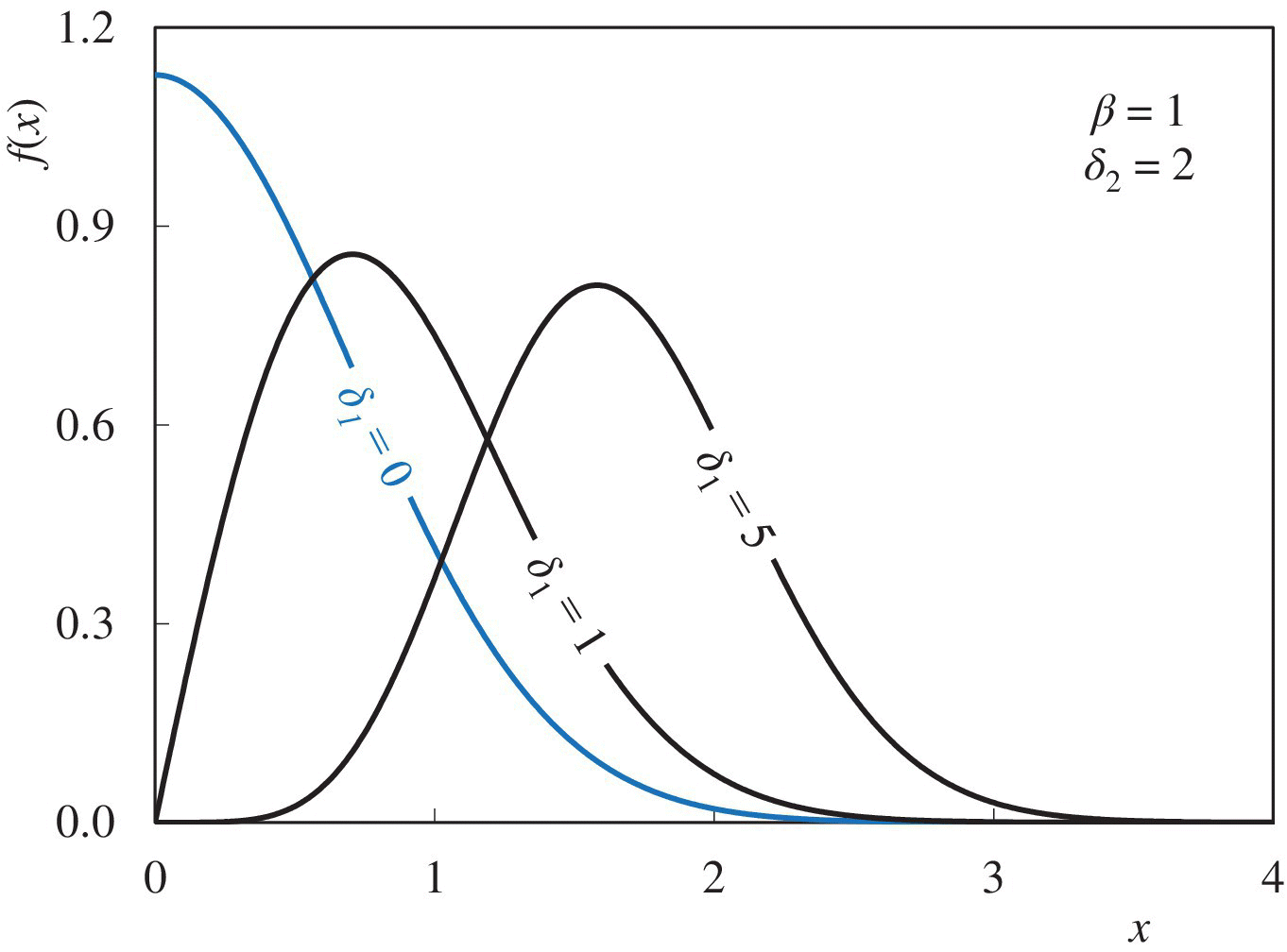
Figure 29.1 Nukiyama–Tanasawa: Effect of δ₁ on shape

Fitting to the C₄ in propane data, in this case, requires that F(x_n) is forced to 1; otherwise the fit in this area is very poor. Doing so sets β, δ₁ and δ₂ to 1.01, 2.954 and 0.948 respectively. With RSS at 0.0779 the fit is poor compared to several alternative distributions.

29.2 Q‐Weibull

Employing a method similar to that used to develop the q‐Gaussian distribution from the normal distribution, the q‐Weibull distribution is developed from the Weibull distribution. It is another in the family of Tsallis distributions.

For q ≥ 1 the PDF is

(29.2)

If q < 1 Equation (29.2) applies only if

(29.3)

If q is set to 1, the distribution reverts to the ...