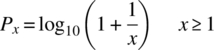Statistics for Process Control Engineers

36Other Discrete Distributions

There are a number of discrete distributions that have no obvious connection to the binomial distribution or its derivatives. They are included here in alphabetical order. The reader might reasonably question the relevance of some to the process industry. Many have been included because they are well known and some explanation is merited as to why they have little application in the process industry. Others included are here simply because some might consider them interesting and identify a use previously not considered.

36.1 Benford

Benford’s Law, also known as the First Digit Law, concerns the frequency at which leading digits occur in datasets. For certain datasets, the probability that a member of the set begins with the digits (x) is

(36.1)

Provided x is an integer the law is applicable to any string of leading digits. More commonly though it is applied to the single leading digit. Figure 36.1 shows the expected Benford distribution. It generally requires that the dataset covers several orders of magnitude.

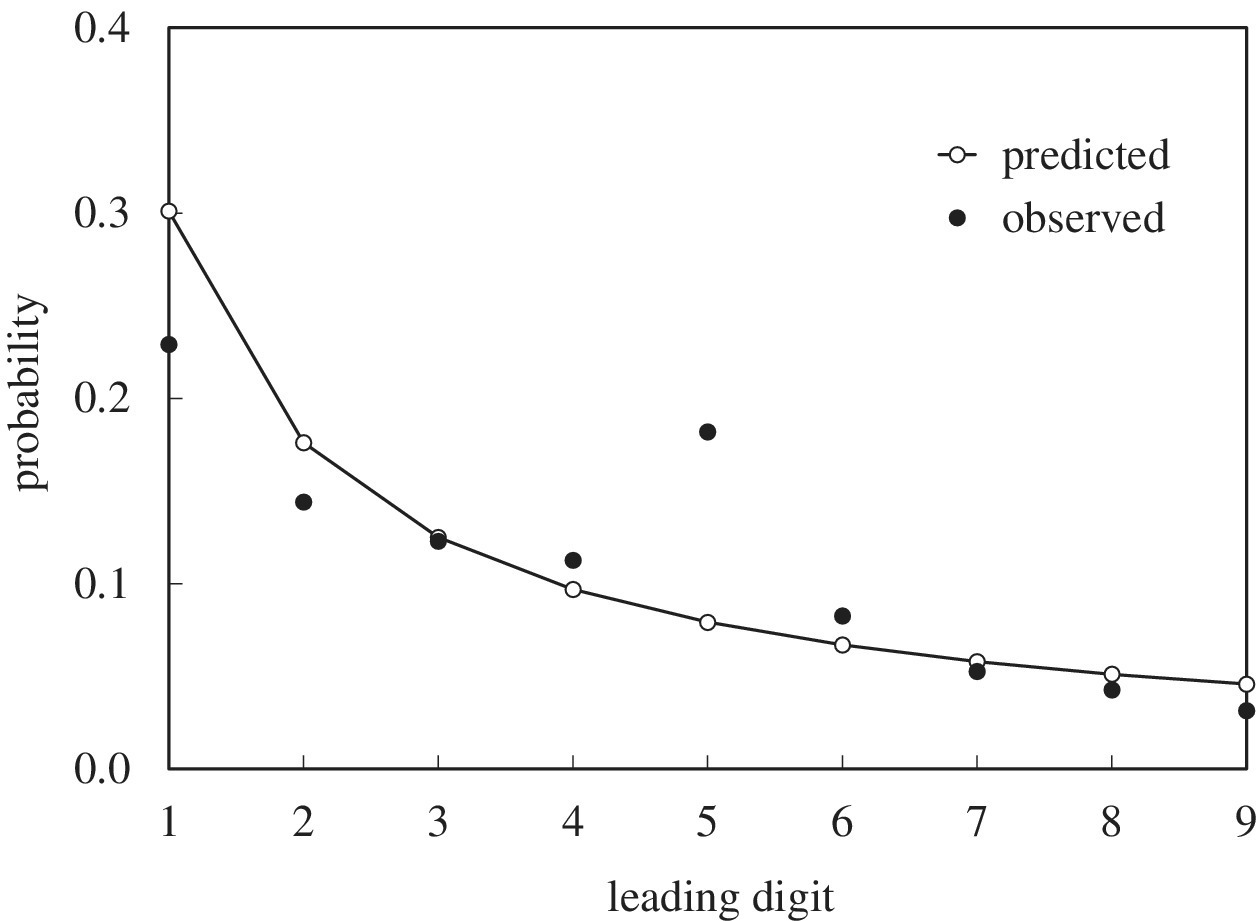
Figure 36.1 Benford: Expected and actual distribution of leading digit in accounts

One application is the detection of fraud in company accounts. Data fabricated by fraudsters might be expected to be uniformly distributed. To help understand ...