Appendix B
The Ergun equation – and beyond
The problem in isolating the ideal regenerator lies not so much with availability of matrix materials as with a lack of basic data for the screening of promising candidates. The data required are heat transfer and flow friction correlations, and these need to cover a range of volume porosities. Friction factor, cf, is correlated to Reynolds number, Nre, relatively easily via a straightforward steady-flow experiment. Corresponding heat transfer correlations pose greater difficulty, possibly explaining why the (NstNpr2/3 – Nre) data of the open literature are confined to spheres and wire screens.
There is a great attraction to being able to express Cf-Nre in terms of geometry and ![]() via first-principles considerations. Early work in this direction by the present writer (Organ 1984) now appears unsatisfactory, but is worth putting in order. Following the earlier attempt, the wire screen is viewed as an array of uniformly spaced cylindrical rods of diameter dw. The algebraic start point is Lamb's expression of 1932 for drag per unit length in ‘creeping’ flow over a cylinder. Lamb's original equation has since been extended by Tomotika and Aoi (1951). The form cited by White (1974) is:
via first-principles considerations. Early work in this direction by the present writer (Organ 1984) now appears unsatisfactory, but is worth putting in order. Following the earlier attempt, the wire screen is viewed as an array of uniformly spaced cylindrical rods of diameter dw. The algebraic start point is Lamb's expression of 1932 for drag per unit length in ‘creeping’ flow over a cylinder. Lamb's original equation has since been extended by Tomotika and Aoi (1951). The form cited by White (1974) is:
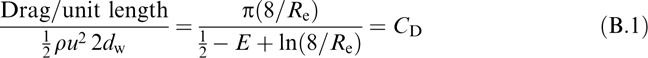
In equation (B.1), E is Euler's constant 0.57721..., cD is coefficient ...
Get Stirling and Pulse-tube Cryo-coolers now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

