Special Functions
8.1 Elliptic Integrals and Functions
8.11 Elliptic integrals
8.110
1. Every integral of the form ![]() , where P(x) is a third- or fourth-degree polynomial, can be reduced to a linear combination of integrals leading to elementary functions and the following three integrals:
, where P(x) is a third- or fourth-degree polynomial, can be reduced to a linear combination of integrals leading to elementary functions and the following three integrals:
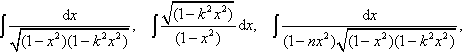
which are called respectively elliptic integrals of the first, second, and third kind in the Legendre normal form. The results of this reduction for the more frequently encountered ...
Get Table of Integrals, Series, and Products, 8th Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

