Table of Integrals, Series, and Products, 8th Edition

8.4–8.5 Bessel Functions and Functions Associated with Them

8.40 Definitions

8.401 Bessel functions Z_v(z) are solutions of the differential equation

$\frac{d^2{Z}_{\nu }}{d{z}^2}+\frac{1}{z}\frac{d{Z}_{\nu }}{dz}+\left(1-\frac{{\nu }^2}{z^2}\right)Z_{\nu }=0$

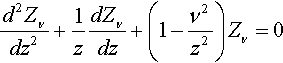  KU 37(1)

Special types of Bessel functions are what are called Bessel functions of the first kind J_v(z), Bessel functions of the second kind Y_v(z) (also called Neumann functions and often written N_v(z)), and Bessel functions of the third kind $H_{\nu }^{(1)}(z)$ and $H_{\nu }^{(2)}(z)$ (also ...