The Multilevel Fast Multipole Algorithm (MLFMA) for Solving Large-Scale Computational Electromagnetics Problems

Appendix

A.1 Limit Part of the 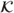Operator

As given in (1.52), the integro-differential operator is commonly separated into principal-value and limit parts as

A.1

where is the solid angle. Specifically, when the observation point is not located on the source . If it is located on the source, however, is determined by the “shape” of the surface, on which is defined. If the surface is planar at , then and

A.2

Derivation of the limit part of the operator is quite straightforward when the source ...