The R Book, 2nd Edition

Chapter 12

Analysis of Covariance

Analysis of covariance (ANCOVA) combines elements from regression and analysis of variance. The response variable is continuous, and there is at least one continuous explanatory variable and at least one categorical explanatory variable. The procedure works like this:

• Fit two or more linear regressions of y against x (one for each level of the factor).
• Estimate different slopes and intercepts for each level.
• Use model simplification (deletion tests) to eliminate unnecessary parameters.

For example, we could use ANCOVA in a medical experiment where the response variable was ‘days to recovery’ and the explanatory variables were ‘smoker or not’ (categorical) and ‘blood cell count’ (continuous). In economics, local unemployment rate might be modelled as a function of country (categorical) and local population size (continuous). Suppose we are modelling weight (the response variable) as a function of sex and age. Sex is a factor with two levels (male and female) and age is a continuous variable. The maximal model therefore has four parameters: two slopes (a slope for males and a slope for females) and two intercepts (one for males and one for females) like this:

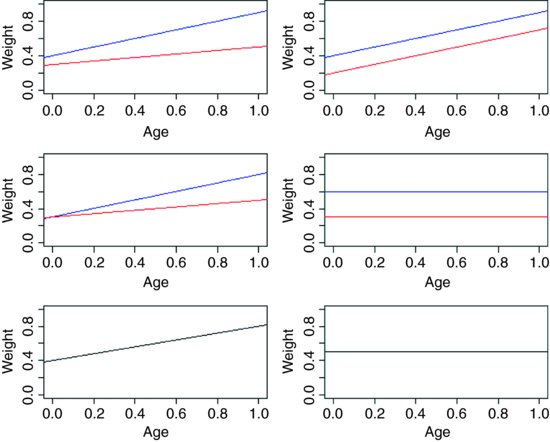
This maximal model is shown in the top left-hand panel. Model simplification is an essential ...