Think DSP

Chapter 2. Harmonics

In this chapter I present several new waveforms; we will look at their spectrums to understand their harmonic structure, which is the set of sinusoids they are made up of.

I’ll also introduce one of the most important phenomena in digital signal processing: aliasing. And I’ll explain a little more about how the Spectrum class works.

The code for this chapter is in chap02.ipynb, which is in the repository for this book (see “Using the Code”). You can also view it at http://tinyurl.com/thinkdsp02.

Triangle Waves

A sinusoid contains only one frequency component, so its spectrum has only one peak. More complicated waveforms, like the violin recording in Figure 1-2, yield DFTs with many peaks. In this section we investigate the relationship between waveforms and their spectrums.

I’ll start with a triangle waveform, which is like a straight-line version of a sinusoid. Figure 2-1 shows a triangle waveform with frequency 200 Hz.

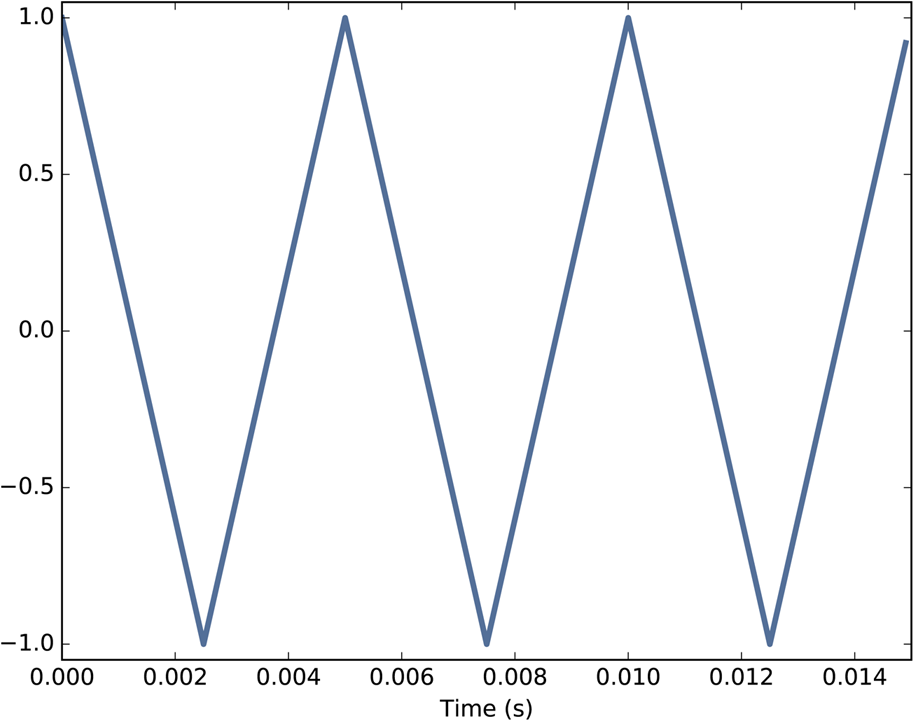
Figure 2-1. Segment of a triangle signal at 200 Hz.

To generate a triangle wave, you can start with a thinkdsp.TriangleSignal:

class TriangleSignal(Sinusoid):
    
    def evaluate(self, ts):
        cycles = self.freq * ts + self.offset / PI2
        frac, _ = np.modf(cycles)
        ys = np.abs(frac - 0.5)
        ys = normalize(unbias(ys), self.amp)
        return ys

TriangleSignal inherits __init__ from Sinusoid, so it takes the same arguments: freq, amp, and offset.

The only difference is evaluate ...