2Vibration of Discrete Systems: Brief Review
2.1 VIBRATION OF A SINGLE‐DEGREE‐OF‐FREEDOM SYSTEM
The number of degrees of freedom of a vibrating system is defined by the minimum number of displacement components required to describe the configuration of the system during vibration. Each system shown in Fig. 2.1 denotes a single‐degree‐of‐freedom system. The essential features of a vibrating system include: (i) a mass m, producing an inertia force: 
; (ii) a spring of stiffness k, producing a resisting force: kx; and (iii) a damping mechanism that dissipates the energy. If the equivalent viscous damping coefficient is denoted as c, the damping force produced is 
.
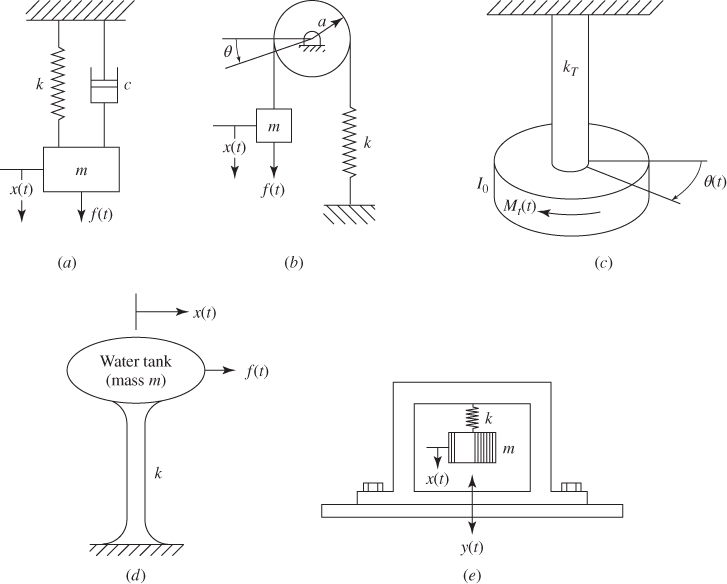
Figure 2.1 Single‐degree‐of‐freedom systems.
2.1.1 Free Vibration
In the absence of damping, the equation of motion of a single‐degree‐of‐freedom system is given by
where 
is the force acting on the mass and 
is the ...
Get Vibration of Continuous Systems, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
