VLSI Digital Signal Processing Systems: Design and Implementation

13.2    PARALLEL MULTIPLIERS

This section considers multipliers that can perform two’s complement multiplication in time O(W) using regular structures, including multiplication with sign extension (derived from Horner’s rule) and Baugh-Wooley multiplication [9]. Two regular implementation styles, carry-ripple and and carry-save array, are introduced.

It has been proved that multiplications cannot be performed in a time smaller than O(log₂W). Such a bound is attainable by the binary-tree and Wallace-tree multipliers (see Appendix E) [10]. However, their corresponding architectures are very irregular.

Let the multiplicand and multiplier be A and B:

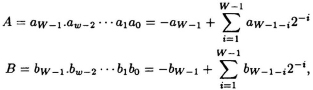
where −1 < A, B < 1 and the case when both A and B is equal to −1 is excluded. The value of their product P = A × B is given by:

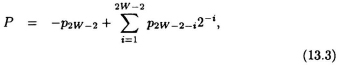
where the radix point is to the right of the msb p_2w−2. Since the product of 2 numbers within [−1, 1) is also in this range, all higher order bits to the left of bit-position 2W − 2 in the result are ignored.

In constant wordlength multiplication, the W − 1 lower order bits in the product P are discarded, and the product is denoted as X ⇐ P = A × B, where

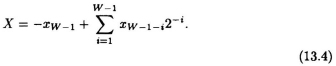
The product X is used when a constant wordlength multiplier ...