Well Test Analysis for Multilayered Reservoirs with Formation Crossflow

Appendix B

Approximate Solution of the Diffusivity Crossflow Problem in n-Layer Reservoirs (Chapter 3)

Suppose a well produces from all layers in an n-layer reservoir at a common wellbore pressure and a constant total rate, q, for $t>0$. Under the assumptions we made, the problem can be described as follows. The equations are

$\begin{array}{c}\hfill \frac{1}{{\eta }_i}\frac{\partial p_i}{\partial t}-\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial p_i}{\partial r}\right)+\frac{{\tilde{k}}_{i-1}}{k_i{h}_i}\left(p_i-p_{i-1}\right)+\frac{{\tilde{k}}_i}{k_i{h}_i}\left(p_i-p_{i+1}\right)=0,\hfill \\ \hfill i=1,2,\dots ,n;{\tilde{k}}_0={\tilde{k}}_n=0\hfill \end{array}$

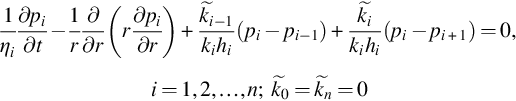  (B.1)

where ${\eta }_i=\frac{k_i}{{\varphi }_i\mu c_t}$ and $\tilde{k}$ is the semipermeability ...