How neural networks learn distributed representations
Deep learning’s effectiveness is often attributed to the ability of neural networks to learn rich representations of data.
 Neurons (source: Pixabay)
Neurons (source: Pixabay)
The concept of distributed representations is often central to deep learning, particularly as it applies to natural language tasks. Those beginning in the field may quickly understand this as simply a vector that represents some piece of data. While this is true, understanding distributed representations at a more conceptual level increases our appreciation of the role they play in making deep learning so effective.
To examine different types of representation, we can do a simple thought exercise. Let’s say we have a bunch of “memory units” to store information about shapes. We can choose to represent each individual shape with a single memory unit, as demonstrated in Figure 1.
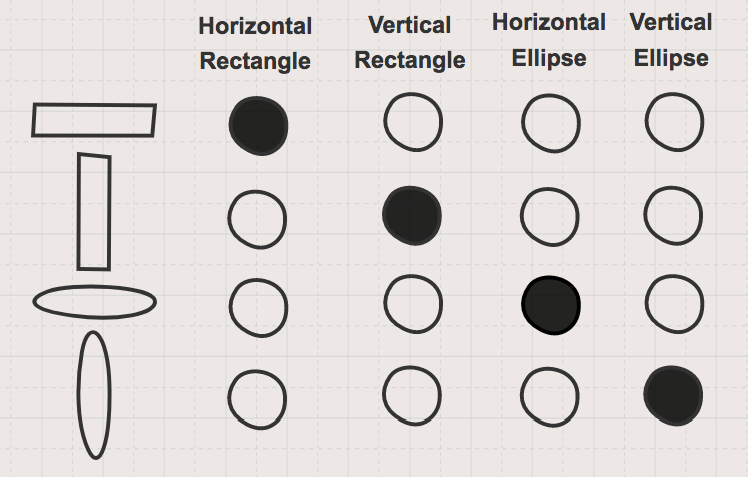
This non-distributed representation, referred to as “sparse” or “local,” is inefficient in multiple ways. First, the dimensionality of our representation will grow as the number of shapes we observe grows. More importantly, it doesn’t provide any information about how these shapes relate to each other. This is the true value of a distributed representation: its ability to capture meaningful “semantic similarity” between between data through concepts.
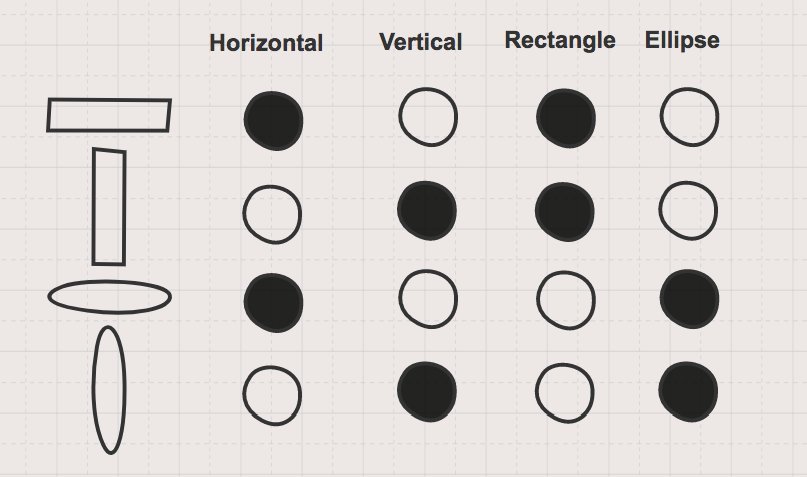
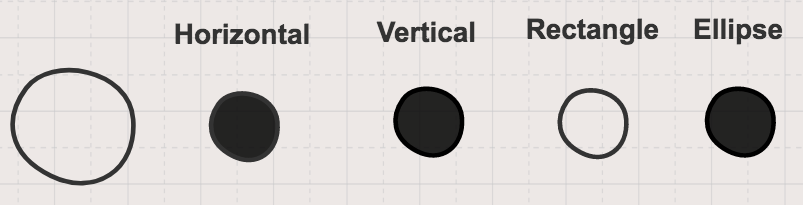
Figure 2 shows a distributed representation of this same set of shapes where information about the shape is represented with multiple “memory units” for concepts related to orientation and shape. Now the “memory units” contain information both about an individual shape and how each shape relates to each other. When we come across a new shape with our distributed representation, such as the circle in Figure 3, we don’t increase the dimensionality and we also know some information about the circle, as it relates to the other shapes, even though we haven’t seen it before.
While this shape example is oversimplified, it serves as a great high-level, abstract introduction to distributed representations. Notice, in the case of our distributed representation for shapes, that we selected four concepts or features (vertical, horizontal, rectangle, ellipse) for our representation. In this case, we were required to know what these important and distinguishing features were beforehand, and in many cases, this is a difficult or impossible thing to know. It is for this reason that feature engineering is such a crucial task in classical machine learning techniques. Finding a good representation of our data is critical to the success of downstream tasks like classification or clustering. One of the reasons that deep learning has seen tremendous success is a neural networks’ ability to learn rich distributed representations of data.
To examine this, we will revisit the problem we tackled in our LSTM tutorial—predicting stock market sentiment from social media posts from StockTwits. In this tutorial, we built a multi-layered LSTM to predict the sentiment of a message from the raw body of text. When processing our message data, we created a mapping of our vocabulary to an integer index.
This mapping of vocabulary to integer is a non-distributed sparse representation of our data. For instance, the word buy is mapped to index 25 and the word long is represented as index 68. Note that this is an equivalent representation to a “one-hot encoded” vector of length vocab_size with a 1 in the index representing the word and a 0 everywhere else. These are two independent representations that have no relational information between the two words despite their semantic similarity when it comes to investing—both words represent a position of owning a stock.
The canonical methodology for learning a distributed representation of words is the Word2Vec model. The Word2Vec skip-gram model, whose architecture is pictured in Figure 4, takes in a single word, passes this to a single linear hidden layer unique to that word, and uses a softmax activation layer to predict the words that occur in a window around it.
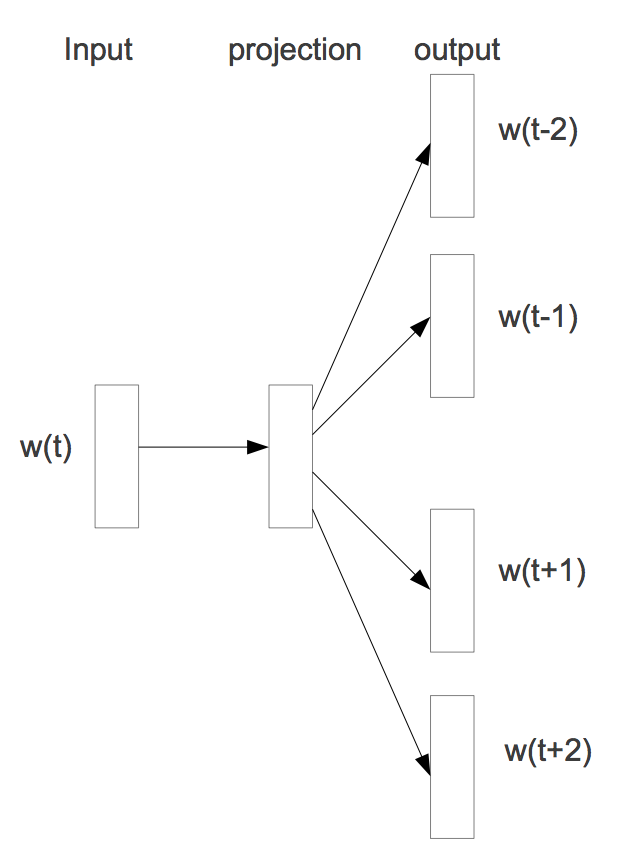
The Word2Vec model uses the J.R. Firth philosophy—“you shall know a word by the company it keeps,” and can be implemented very easily in TensorFlow. By learning hidden weights, which will be used as our distributed representation, words that appear in similar context will have a similar representation. Word2Vec is a model designed specifically for learning distributed representations of words, also called “word embeddings,” from their context. Oftentimes, these embeddings are pre trained with Word2Vec and then used as inputs to other models performing language tasks.
Alternatively, distributed representations can be learned in an end-to-end fashion as part of the model training process for an arbitrary task. This is how we learned our word embedding in our stock market sentiment LSTM model. Recall the model architecture (see Figure 5), where we input our sparse representation of words into an embedding layer.
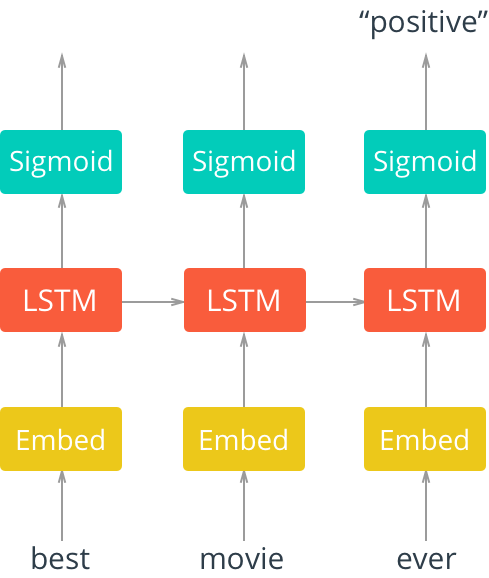
Trained under this paradigm, distributed representations will specifically learn to represent items as they relate to the learning task—in our case, our distributed representation should specifically learn semantic context around sentiments of words. We can examine this by extracting our word embeddings and looking at some examples.
We visualize the relationship between a few “bearish-bullish pairs” by reducing the dimensionality of our representations using tSNE (see Figure 6). Note the concept of sentiment represented by the left-to-right direction between word pairs (i.e., bearish vs. bullish, overvalued vs. undervalued, short vs. long, etc.).

While these aren’t perfect—ideally, we would want to see the pairings more vertically aligned, and we also have some pairs where sentiment is reversed—they are pretty good given limited training. Our model’s ability to learn this type of representation is a major reason it is able to achieve high accuracy when predicting sentiment.
A neural network’s ability to learn distributed representation of data is one of the main reasons that deep learning is so effective for so many different types of problems. The power and beauty of this concept makes representation learning one of the most exciting and active areas of deep learning research. Methods for learning shared representations across multiple modals (e.g., words and images, words in different languages) are enabling advancements in image captioning and translation. We can be sure that better understanding these types of representations will continue to be a major factor in driving AI forward.
This post is a collaboration between O’Reilly and TensorFlow. See our statement of editorial independence.
