How to get superior text processing in Python with Pynini
Regular expressions are the standard for string processing, but did you know you can often get better text untangling with Pynini's finite-state transducers?
 Dish (source: olafpictures via Pixabay)
Dish (source: olafpictures via Pixabay)
It’s hard to beat regular expressions for basic string processing. But for many problems, including some deceptively simple ones, we can get better performance with finite-state transducers (or FSTs). FSTs are simply state machines which, as the name suggests, have a finite number of states. But before we talk about all the things you can do with FSTs, from fast text annotation—with none of the catastrophic worst-case behavior of regular expressions—to simple natural language generation, or even speech recognition, let’s explore what a state machine is, what they have to do with regular expressions.
From gumball machines to state machines
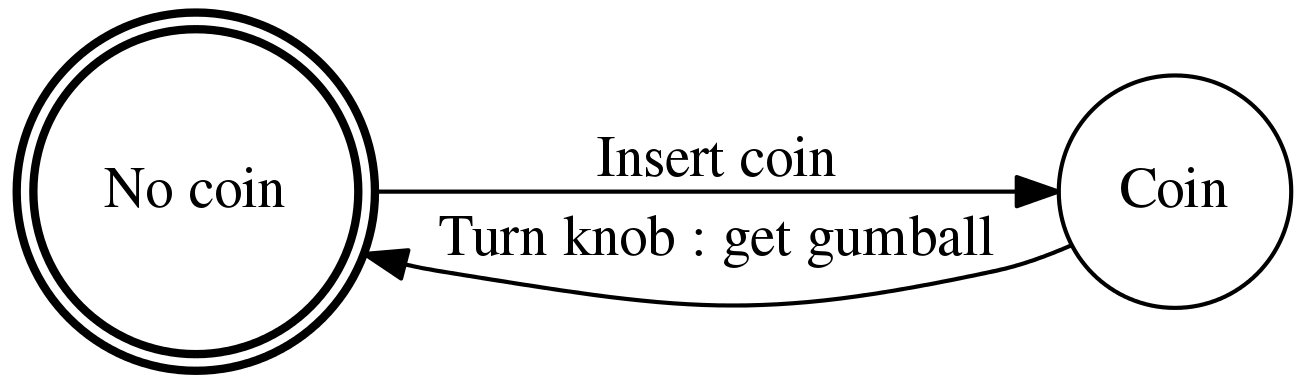
A state machine is any piece of software or hardware whose behavior can be described in terms of transitions between states. For instance, a gumball machine can be in one of two states:
- the coin slot is empty
- the coin slot has a quarter in it
In this gumball machine, there are two transitions:
- inserting a coin into the machine
- turning the knob, hopefully yielding a tasty gumball
And, transition (A) is only possible when the machine is in state (0)—when the slot is empty—and transition (B) is only possible when the machine is in state (1)—when a coin is in the slot. The following image depicts the states and transitions of our gumball machine with circles and arrows, respectively.
From state machines to regular expressions
A regular expression matcher can also be thought of as a state machine. Consider the regular expression /ba+/, which matches ba, baa, baaa, and so on. It is described by the following state machine:
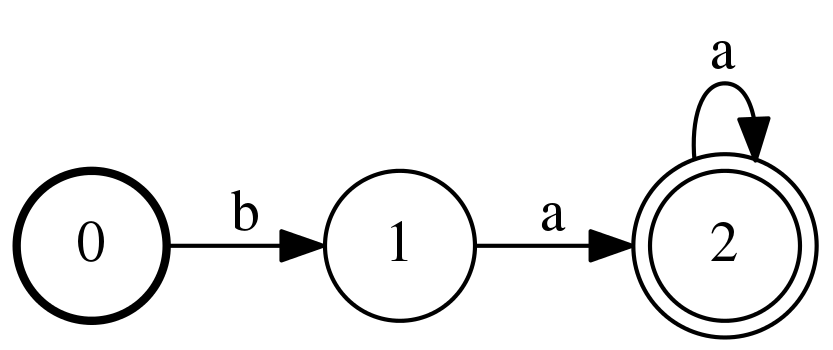
/ba+/; the thick circle on the 0 state indicates the start state, and the double circle on the 2 state indicates the final state. Image credit: Kyle Gorman
We say that a string matches the regular expression if and only if it corresponds to a path through the corresponding state machine. To define a path, we must first define the following properties:
- At least one state must be designated as a start state (indicated in the diagram with a thick border)
- At least one state must be designated as a final state (indicated in the diagram with a double border)
- Each transition must be associated with a label, here a character like b (indicated in the diagram by labels along the arrows)
Then, a path through the state machine is a set of transitions beginning at a start state and ending at a final state. By concatenating the transition labels, we also obtain the matched string. For instance, if the string is baa, then we take the following transitions:
- State 0 to state 1 with label b
- State 1 to state 2 with label a
- State 2 to state 2 with label a
Since 0 is a start state and 2 is a final state, this string is a match for the regular expression. However, b does not correspond to a valid path because the path would terminate at state 1, which is not a final state; and, moo does not correspond to a valid path simply because there is no transition labeled m or o.
This type of state machine is known as a finite-state acceptor (or FSA) because it has a finite number of states and it either “accepts” (matches) or “rejects” a string. And all regular expression engines use FSAs—either explicitly or implicitly—for matching.
From regular expressions to finite-state transducers
Finite-state transducers (FSTs) are a generalization of FSAs, where each transition is associated with a pair of labels. Then each pair forms part of not one string but two, an input string and an output string. As a result, transducers model relations between pairs of strings. FSAs can be thought of as a special case in which every transition has the same input and output label.
Thanks to decades of computer science research, there are many efficient algorithms for compiling, combining, optimizing, and searching FSTs, much of this developed for speech recognition, but here we show how FSTs are simple and efficient tools for annotating, and generating natural language.
Application 1: String tagging
Imagine that we have a collection of texts and we wish to place XML-style tags around any mention of a various types of fine cheese. So, for instance, given a string like
input_string = "Do you have Camembert or Edam?"
and a list of fine cheeses,
cheeses = ("Boursin", "Camembert", "Cheddar", "Edam", "Gruyere",
"Ilchester", "Jarlsberg", "Red Leicester", "Stilton")
we would produce
output_string = "Do you have <cheese>Camembert</cheese> or <cheese>Edam</cheese>"
Now, we could simply compile this list directly into a regular expression using Python’s re library:
re_target = re.compile("(" + "|".join(re.escape(ch) for ch in cheeses) + ")")
However, the resulting regular expression will have an unpleasant property—non-determinism—leading to inefficient matching. As a result, the re module (and many other regular expression engines) is forced to fall back to a “back-tracking” strategy with catastrophic worst-case behavior.
FSA for efficient matching vs. regular expressions
However, it is easy to construct a deterministic FSA using Pynini, one of several open-source finite-state transducer libraries developed at Google.
fst_target = pynini.string_map(cheeses)
This function constructs an FSA with a prefix tree (or trie) topology, guaranteeing that the resulting FSA will be deterministic.
Now, how do we use this object to insert brackets? With Python’s re objects, we have several options, including a single pass of string substitution with re.sub and a back-reference. With our deterministic FSA fst_target, the simplest solution is to create an FST which represents the substitution as a string-to-string rewrite relation, as follows. First, we construct transducers which insert the left and right tags; i.e., they literally map from the empty string to the tag.
ltag = pynini.transducer("", "<cheese>")
rtag = pynini.transducer("", "</cheese>")
We then build the substitution transducer by concatenating these transducers to the left and right of the deterministic FSA we are trying to match (note that + is overloaded to perform FST concatenation).
substitution = ltag + fst_target + rtag
Now, this transducer represents the tag insertion relation itself. But as written, we cannot apply it to arbitrary strings, for it does not match any part of a string which is not part of a cheese name. To complete the task, we need an FST which passes through any part of a string which does not match. For this we use cdrewrite (short for “context-dependent rewrite”). This function takes (minimally) four arguments:
- The substitution transducer,
- A left context for the substitution (cf. lookbehind assertions),
- A right context for the substitution (cf. lookahead assertions), and
- an FSA representing the alphabet of characters we expect to find in the input
We have already constructed (1), and as there are no restrictions on where the context rule applies, we provide empty strings for (2–3). For (4), we use all valid bytes—except the null byte \0 —and escape the reserved characters [, \, and ].
chars = ([chr(i) for i in xrange(1, 91)] +
["\[", "\\", "\]"] +
[chr(i) for i in xrange(94, 256)])
sigma_star = pynini.string_map(chars).closure()
Finally, we construct the tagger transducer itself.
rewrite = pynini.cdrewrite(substitution, "", "", sigma_star)
Then, all that remains is to apply this to a string. The simplest way to do so is to compose a string and the rewrite transducer, then convert the resulting path back into a string.
output = pynini.compose(input_string, rewrite).stringify()
Application 2: Plural rules
Consider an application where one is generating text such as, “The current temperature in New York is 25 degrees”. Typically one would do this from a template such as:
The current temperature in __ is __ degrees
This works fine if one fills in the first blank with the name of a location and the second blank with a number. But what if it’s really cold in New York and the thermometer shows 1° (Fahrenheit)? One does not want this:
The current temperature in New York is 1 degrees
So one needs to have rules that know how to inflect the unit appropriately given the context. The Unicode Consortium has some guidelines for this; they primarily specify how many “plural” forms different languages have and in which circumstances one uses each. From a linguistic point of view the specifications are sometimes nonsensical, but they are widely used and are useful for adding support for new languages.
For handling degrees, we can assume that the default is the plural form, in which case we must singularize the plural form in certain contexts. For the word degrees and many other cases, it’s just a matter of stripping off the final s, but for a word ending in -ches (such as inches) one would want to strip off the es, and for feet and pence the necessary changes are irregular (foot, penny).
Pynini simplicity vs. special purpose Python function
One could of course take care of this with a special purpose Python function, but here we consider how simple this is in Pynini. We start by defining a singular_map to handle irregular cases, plus the general cases:
singular_map = pynini.union(
pynini.transducer("feet", "foot"),
pynini.transducer("pence", "penny"),
# Any sequence of bytes ending in "ches" strips the "es";
# the last argument -1 is a "weight" that gives this analysis
# a higher priority, if it matches the input.
sigma_star + pynini.transducer("ches", "ch", -1),
# Any sequence of bytes ending in "s" strips the "s".
sigma_star + pynini.transducer("s", ""))
Then as before we can define a context-dependent rewrite rule that performs the singularization just in case the unit is preceded by ” 1 “. We define the right context for the application of the rule rc as punctuation, space, or “[EOS]“, a special symbol for the end-of-string.
rc = pynini.union(".", ",", "!", ";", "?", " ", "[EOS]")
singularize = pynini.cdrewrite(singular_Map, " 1 ", rc, sigma_star)
Then we can define a convenience function to apply this rule…
def singularize(string):
return pynini.shortestpath(
pynini.compose(string.strip(), singularize)).stringify()
…and use it like so:
>>> singularize("The current temperature in New York is 1 degrees")
>>> "The current temperature in New York is 1 degree"
>>> singularize("That measures 1 feet")
>>> "That measures 1 foot"
>>> singularize("That measures 1.2 feet")
>>> "That measures 1.2 feet"
>>> singularize("That costs just 1 pence")
>>> "That costs just 1 penny"
One can handle other languages by changing the rules appropriately—for example, in Russian, which has more complex pluralization rules, one needs several different forms, not just singular and plural—and by changing the conditions under which the various rules apply.
We’ve only begun to scratch the surface of what can be done with FSTs. When we use them to mark up text, we can compose (i.e., chain) a cascade of multiple FSTs into a single machine, an important trick for information extraction. This trick is also used in speech synthesis, where a huge series of rules handling morphology (like the example above), the pronunciations of numbers, dates, times, prices, and the like are all built into a single, all-powerful, automatically optimized FST.
FSTs are also being used to encode probability models over sequences. Speech recognizers are essentially a cascade of WFSTs, mapping from audio to phones, phones to words, and words to utterances. Once such a model is built, we can efficiently search for the highest-probability outcome using the shortest-path algorithm. So whenever you talk to your smartphone, or it talks back, you’re seeing FSTs untangling text in real time.
