Operations in Pandas

One of the essential pieces of NumPy is the ability to perform quick elementwise operations, both with basic arithmetic (addition, subtraction, multiplication, etc.) and with more sophisticated operations (trigonometric functions, exponential and logarithmic functions, etc.). Pandas inherits much of this functionality from NumPy, and the universal functions (ufuncs for short) which we introduced in section X.X are key to this.

Pandas includes a couple useful twists, however: for unary operations like negation and trigonometric functions, these ufuncs will preserve index and column labels in the output, and for binary operations such as addition and multiplication, Pandas will automatically align indices when passing the objects to the ufunc. This means that keeping the context of data, and combining data from different sources – both potentially error-prone tasks with raw NumPy arrays – become essentially foolproof with Pandas. We will additionally see that there are well-defined operations between one-dimensional Series structures and two-dimensional DataFrame structures.

Ufuncs: Index Preservation

Because Pandas is designed to work with NumPy, any NumPy ufunc will work on pandas Series and DataFrame objects. Lets start by defining a simple Series and DataFrame on which to demonstrate this:

import pandas as pd
import numpy as np

rng = np.random.RandomState(42)
ser = pd.Series(rng.randint(0, 10, 4))
ser

df = pd.DataFrame(rng.randint(0, 10, (3, 4)),
							columns=['A', 'B', 'C', 'D'])
df

If we apply a NumPy ufunc on either of these objects, the result will be another Pandas object with the indices preserved:

np.exp(ser)

Or, for a slightly more complex calculation:

np.sin(df * np.pi / 4)

Any of the ufuncs discussed in Section X.X can be used in a similar manner.

UFuncs: Index Alignment

For binary operations on two Series or DataFrame objects, Pandas will align indices in the process of performing the operation. This is very convenient when working with incomplete data, as we’ll see in some of the examples below.

Index Alignment in Series

As an example, suppose we are combinging two different data sources, and find only the top three US states by area and the top three US states by population:

area = pd.Series({'Alaska': 1723337, 'Texas': 695662,
							'California': 423967}, name='area')
population = pd.Series({'California': 38332521, 'Texas': 26448193,
										'New York': 19651127}, name='population')

Let’s see what happens when we divide these to compute the population density:

population / area

The resulting array contains the union of indices of the two input arrays, which could be determined using standard Python set arithmetic on these indices:

area.index | population.index

Any item for which one or the other does not have an entry is marked by NaN, or “Not a Number”, which is how Pandas marks missing data (see further discussion of missing data in Section X.X). This index matching is implemented this way for any of Pythons built-in arithmetic expressions; any missing values are filled-in with NaN by default:

A = pd.Series([2, 4, 6], index=[0, 1, 2])
B = pd.Series([1, 3, 5], index=[1, 2, 3])
A + B

If filling-in NaN values is not the desired behavior, the fill value can be modified using appropriate object methods in place of the operators. For example, calling A.add(B) is equivalent to calling A + B, but allows optional explicit specification of the fill value:

A.add(B, fill_value=0)

Index Alignment in DataFrame

A similar type of alingment takes place for both columns and indices when performing operations on dataframes:

A = pd.DataFrame(rng.randint(0, 20, (2, 2)),
						columns=list('AB'))
A

B = pd.DataFrame(rng.randint(0, 10, (3, 3)),
						columns=list('BAC'))
B

A + B

Notice that indices are aligned correctly irrespective of their order in the two objects, and indices in the result are sorted. Similarly to the case of the Series, we can use the associated object’s arithmetic method and pass any desired fill_value to be used in place of missing entries:

A.add(B, fill_value=np.mean(A.values))

A table of Python operators and their equivalent Pandas object methods follows:

Operator	Pandas Method(s)
+	add()
-	sub(), subtract()
*	mul(), multiply()
/	truediv(), div(), divide()
//	floordiv()
%	mod()
**	pow()

Ufuncs: Operations between DataFrame and Series

When performing operations between a DataFrame and a Series, the index and column alignment is similarly maintained. Operations between a DataFrame and a Series are similar to operations between a 2D and 1D NumPy array. Consider one common operation, where we find the difference of a 2D array and one of its rows:

A = rng.randint(10, size=(3, 4))
A

A - A[0]

According to NumPy’s broadcasting rules (see Section X.X), subtration between a two-dimensional array and one of its rows is applied row-wise.

In Pandas, the convention similarly operates row-wise by default:

df = pd.DataFrame(A, columns=list('QRST'))
df - df.iloc[0]

If you would instead like to operate column-wise, you can use the object methods mentioned above, while specifying the axis keyword:

df.subtract(df['R'], axis=0)

Note that these DataFrame/Series operations, like the operations discussed above, will automatically align indices between the two elements:

halfrow = df.iloc[0, ::2]
halfrow

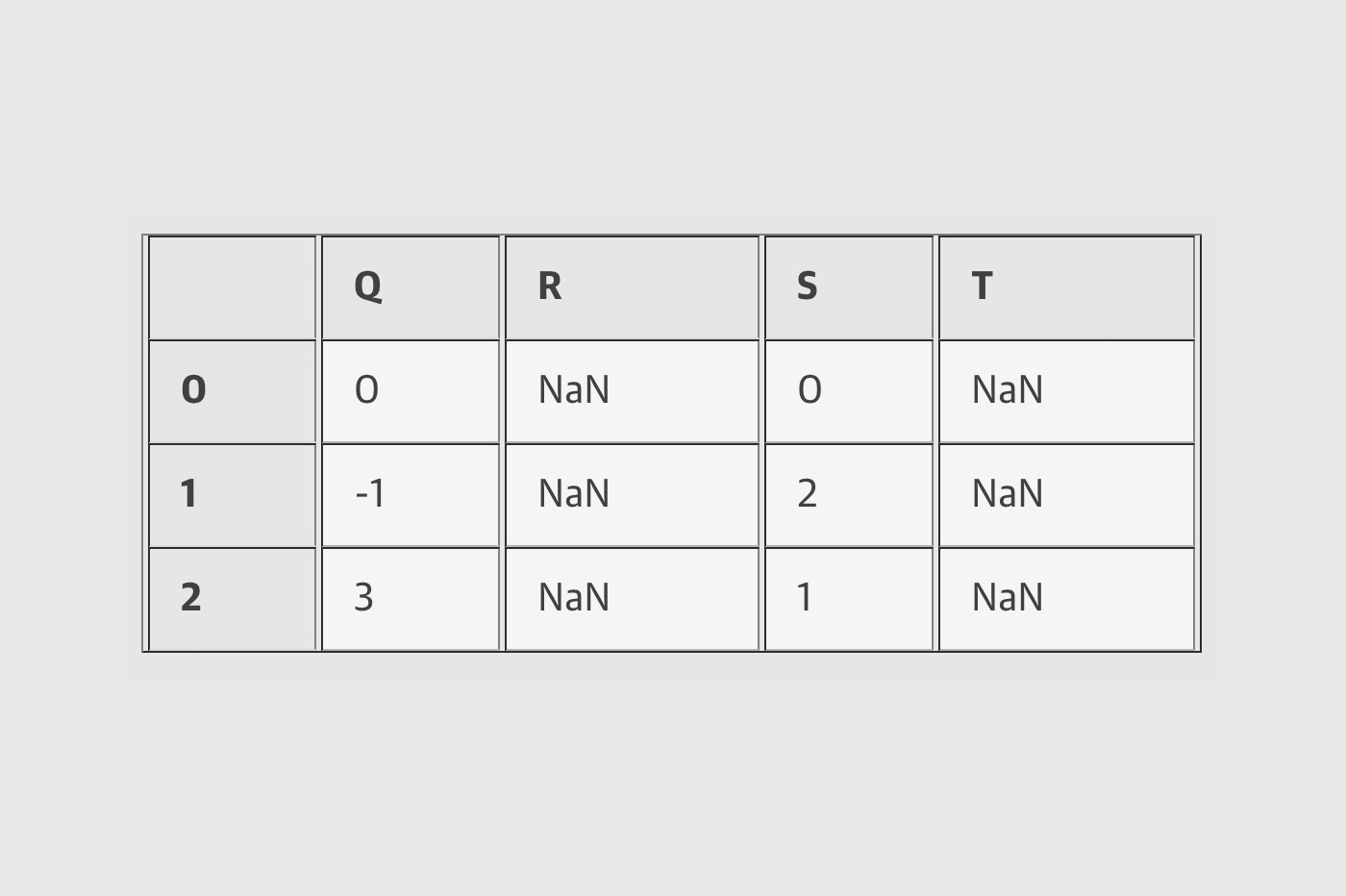
df - halfrow

This preservation and alignment of indices and columns means that operations on data in Pandas will always maintain the data context, which prevents the types of silly errors that might come up when working with heterogeneous data in raw NumPy arrays.

Summary

We’ve shown that standard NumPy ufuncs will operate element-by-element on Pandas objects, with some additional useful functionality: they preserve index and column names, and automatically align different sets of indices and columns. Like the basic indexing and selection operations we saw in the previous section, these types of element-wise operations on Series and DataFrames form the building blocks of many more sophisticated data processing examples to come. The index alignment operations, in particular, sometimes lead to a state where values are missing from the resulting arrays. In the next section we will discuss in detail how Pandas chooses to handle such missing values.