Reinforcement learning explained
Learning to act based on long-term payoffs.
 Maze. (source: Adam Heath on Flickr)
Maze. (source: Adam Heath on Flickr)
A robot takes a big step forward, then falls. The next time, it takes a smaller step and is able to hold its balance. The robot tries variations like this many times; eventually, it learns the right size of steps to take and walks steadily. It has succeeded.
What we see here is called reinforcement learning. It directly connects a robot’s action with an outcome, without the robot having to learn a complex relationship between its action and results. The robot learns how to walk based on reward (staying on balance) and punishment (falling). This feedback is considered “reinforcement” for doing or not doing an action.
Another example of reinforcement learning can be found when playing the game Go. If the computer player puts down its white piece at a location, then gets surrounded by the black pieces and loses that space, it is punished for taking such a move. After being beaten a few times, the computer player will avoid putting the white piece in that location when black pieces are around.
Reinforcement learning, in a simplistic definition, is learning best actions based on reward or punishment.
There are three basic concepts in reinforcement learning: state, action, and reward. The state describes the current situation. For a robot that is learning to walk, the state is the position of its two legs. For a Go program, the state is the positions of all the pieces on the board.
Action is what an agent can do in each state. Given the state, or positions of its two legs, a robot can take steps within a certain distance. There are typically finite (or a fixed range of) actions an agent can take. For example, a robot stride can only be, say, 0.01 meter to 1 meter. The Go program can only put down its piece in one of 19 x 19 (that is 361) positions.
When a robot takes an action in a state, it receives a reward. Here the term “reward” is an abstract concept that describes feedback from the environment. A reward can be positive or negative. When the reward is positive, it is corresponding to our normal meaning of reward. When the reward is negative, it is corresponding to what we usually call “punishment.”
Each of these concepts seem simple and straightforward: Once we know the state, we choose an action that (hopefully) leads to positive reward. But the reality is more complex.
Consider this example: a robot learns to go through a maze. When the robot takes one step to the right, it reaches an open location, but when it takes one step to the left, it also reaches an open location. After going left for three steps, the robot hits a wall. Looking back, taking the left step at location 1 is a bad idea (bad action). How would the robot use the reward at each location (state) to learn how to get through the maze (which is the ultimate goal)?
“Real” reinforcement learning, or the version used as a machine learning method today, concerns itself with the long-term reward, not just the immediate reward.
The long-term reward is learned when an agent interacts with an environment through many trials and errors. The robot that is running through the maze remembers every wall it hits. In the end, it remembers the previous actions that lead to dead ends. It also remembers the path (that is, a sequence of actions) that leads it successfully through the maze. The essential goal of reinforcement learning is learning a sequence of actions that lead to a long-term reward. An agent learns that sequence by interacting with the environment and observing the rewards in every state.
How does an agent know what the desired long-term payoff should be? The secret lies in a Q-table (or Q function). It’s a lookup table for rewards associated with every state-action pair. Each cell in this table records a value called a Q-value. It is a representation of the long-term reward an agent would receive when taking this action at this particular state, followed by taking the best path possible afterward.
How does the agent learn about this long-term Q-value reward? It turns out, the agent does not need to solve a complex mathematical function. There is a simple procedure to learn all the Q-values called Q-learning. Reinforcement learning is essentially learning about Q-values while taking actions.
Q-learning: A commonly used reinforcement learning method
Q-learning is the most commonly used reinforcement learning method, where Q stands for the long-term value of an action. Q-learning is about learning Q-values through observations.
The procedure for Q-learning is:
In the beginning, the agent initializes Q-values to 0 for every state-action pair. More precisely, Q(s,a) = 0 for all states s and actions a. This is essentially saying we have no information on long-term reward for each state-action pair.
After the agent starts learning, it takes an action a in state s and receives reward r. It also observes that the state has changed to a new state s’. The agent will update Q(s,a) with this formula:
Q(s,a) = (1-learning_rate)Q(s,a) + learning_rate (r+ discount_rate max_a Q(s’,a))
The learning rate is a number between 0 and 1. It is a weight given to the new information versus the old information. The new long-term reward is the current reward, r, plus all future rewards in the next state, s’, and later states, assuming this agent always takes its best actions in the future. The future rewards are discounted by a discount rate between 0 and 1, meaning future rewards are not as valuable as the reward now.
In this updating method, Q carries memory from the past and takes into account all future steps. Note that we use the maximized Q-value for the new state, assuming we always follow the optimal path afterward. As the agent visits all the states and tries different actions, it eventually learns the optimal Q-values for all possible state-action pairs. Then it can derive the action in every state that is optimal for the long term.
A simple example can be seen with the following maze robot:
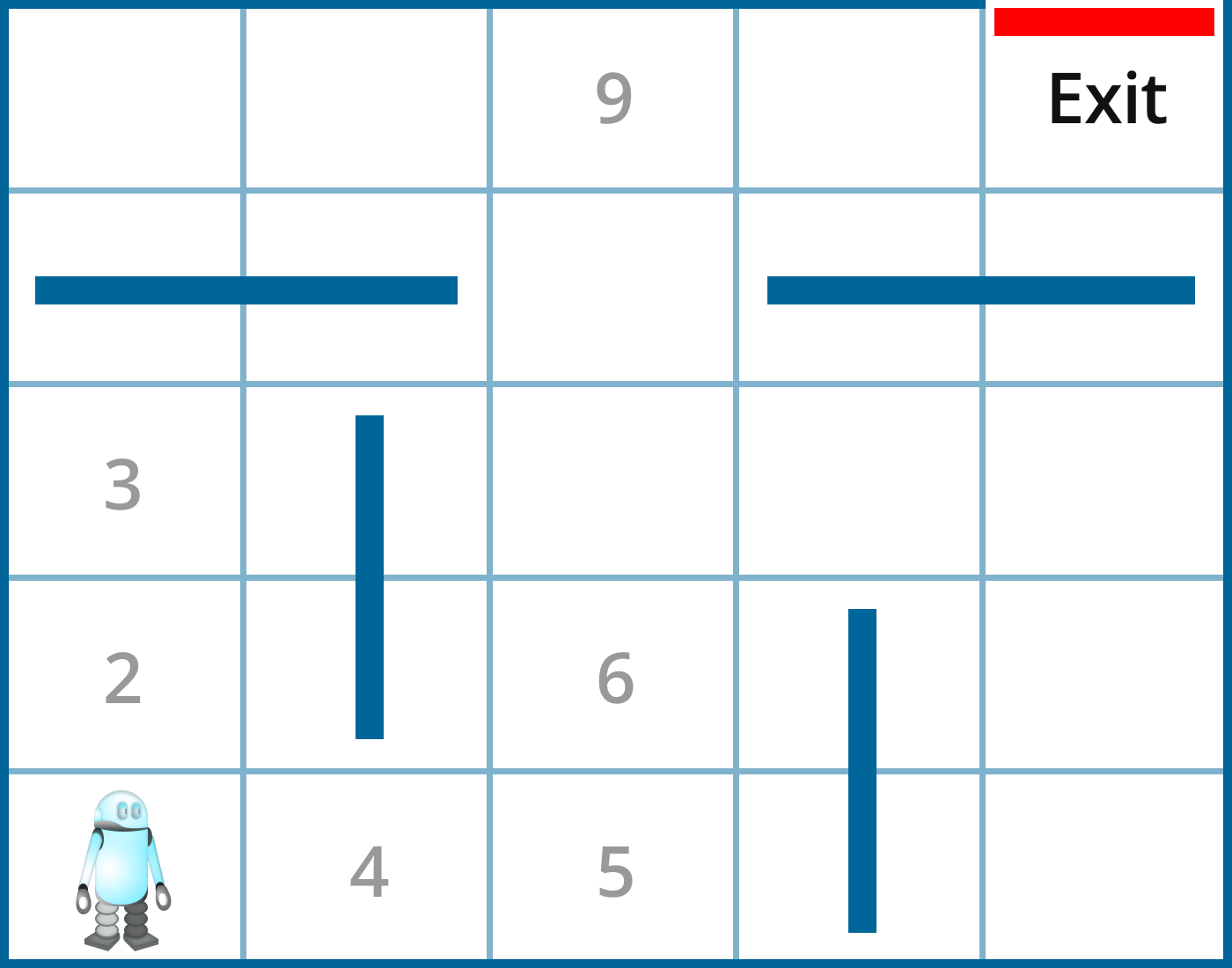
The robot starts from the lower left corner of the maze. Each location (state) is indicated by a number. There are four action choices (left, right, up, down), but in certain states, action choices are limited. For example, in state 1 (initial state), the robot has only two action choices: up or right. In state 4, it has three action choices: left, right, or up. When the robot hits a wall, it receives reward -1. When it reaches an open location, it receives reward 0. When it reaches the exit, it receives reward 100. However, note that this one-time reward is very different from Q-values. In fact, we have
Q(4, left) = 0.8 x 0+ 0.2 (0+0.9 Q(1,right)) and
Q(4, right) = 0.8 x 0+ 0.2 (0+0.9 Q(5,up))
Where the learning rate is 0.2 and discount rate is 0.9. The best action in state 1 is right, and the best action in state 5 is up. Q(1,right) and Q(5,up) have different values because it takes more steps from state 1 than state 5 to reach the exit. Since we discount future rewards, we discount the added steps to reach the goal. Thus Q(5,up) has a higher value than Q(1,right). For this reason, Q(4,right) has a higher value than Q(4, left). Thus, the best action in state 4 is going right.
Q-learning requires the agent try many times to visit all possible state-action pairs. Only then does the agent have a complete picture of the world. Q-values represent the optimal values when taking the best sequence of actions. This sequence of actions is also called “policy.”
A fundamental question we face is: is it possible for an agent to learn all the Q-values when it explores the actions possible in a given environment? In other words, is such learning feasible? The answer is yes if we assume the world responds to actions. In other words, the state changes based on an action. This assumption is called the Markov Decision Process (MDP). It assumes that the next state depends on the previous state and the action taken. Based on this assumption, all possible states can eventually be visited, and the long-term value (Q-value) of every state-action pair can be determined.
Imagine that we live in a random universe where our actions have no impact on what happens next, then reinforcement learning (Q-learning) would break down. After many times of trying, we’d have to throw in the towel. Fortunately, our universe is much more predictable. When a Go player puts down a piece on the board, the board position is clear in the next round. Our agent interacts with the environment and shapes it through its actions. The exact impact of our agent’s action on the state is typically straightforward. The new state is immediately observable. The robot can tell where it ends up.
Common techniques of reinforcement learning
The essential technique of reinforcement learning is exploration versus exploitation. An agent learns about the value of Q(s,a) in state s for every action a. Since the agent needs to get a high reward, it can choose the action that leads to the highest reward based on current information (exploitation), or keep trying new actions, hoping it brings even higher reward (exploration). When an agent is learning online (in real time), the balance of these two strategies is very important. That’s because learning in real time means the agent has to maintain its own survival (when exploring a cave or fighting in a combat) versus finding the best move. It is less of a concern when an agent is learning offline (meaning not in real time). In machine learning terms, offline learning means an agent processes information without interacting with the world. In such cases, the price to pay for failing (like hitting a wall, or being defeated in a game) is little when it can experiment with (explore) many different actions without worrying about the consequences.
The performance of Q-learning depends on visiting all state-action pairs in order to learn the correct Q-values. This can be easily achieved with a small number of states. In the real world, however, the number of states can be very large, particularly when there are multiple agents in the system. For example, in a maze game, a robot has at most 1,000 states (locations); this grows to 1,000,000 when it is in a game against another robot, where the state represents the joint location of two robots (1,000 x 1,000).
When the state space is large, it is not efficient to wait until we visit all state-actions pairs. A faster way to learn is called the Monte Carlo method. In statistics, the Monte Carlo method derives an average through repeated sampling. In reinforcement learning, the Monte Carlo method is used to derive Q-values after repeatedly seeing the same state-action pair. It sets the Q-value, Q(s,a), as the average reward after many visits to the same state-action pair (s, a). This method removes the need for using a learning rate or a discount rate. It depends only on large numbers of simulations. Due to its simplicity, this method has become very popular. It has been used by AlphaGo after playing many games against itself to learn about the best moves.
Another way to reduce the number of states is by using a neural network, where the inputs are states and outputs are actions, or Q-values associated with each action. A deep neural network has the power to dramatically simplify the representation of states through hidden layers. In this Nature paper on deep reinforcement learning used with Atari games, the whole game board is mapped by a convolutional neural network to determine Q-values.
What is reinforcement learning good for?
Reinforcement learning is good for situations where information about the world is very limited: there is no given map of the world. We have to learn our actions by interacting with the environment: trial and error is required. For example, a Go program cannot calculate all possible future states, which could be 10^170, while the universe is only 10^17 seconds old. This means even if the computer can compute one billion (10^9) possible game boards (states) in a second, it will take longer than the age of the universe to finish that calculation.
Since we cannot enumerate all possible situations (and optimize our actions accordingly), we have to learn through the process of taking actions. Once an action is taken, we can immediately observe the results and change our action the next time.
Recent applications
Reinforcement learning historically was mostly applied to robot control and simple board games, such as backgammon. Recently, it achieved a lot of momentum by combining with deep learning, which simplifies the states (when the number of states is very large). Current applications of reinforcement learning include:
1. Playing the board game Go.
The most successful example is AlphaGo, a computer program that won against the second best human player in the world. AlphaGo uses reinforcement learning to learn about its next move based on current board position. The board position is simplified through a convolutional neural network, which then produces actions as outputs.
2. Computer games.
Most recently, playing Atari Games.
3. Robot control.
Robots can learn to walk, run, dance, fly, play ping pong or stack Legos with reinforcement learning.
4. Online advertising.
A computer program can use reinforcement learning to select an ad to show to a user at the right time, or with the right format.
5. Dialogue generation.
A conversational agent selects a sentence to say based on a forward-looking, long-term reward. This makes the dialogue more engaging and longer lasting. For example, instead of saying, “I am 16” in response to the question, “How old are you?”, the program can say, “I am 16. Why are you asking?”
Getting started with reinforcement learning
OpenAI provides a reinforcement learning benchmarking toolkit called OpenAI Gym. It has sample code and can help a beginner to get started. The CartPole problem is a fun problem to start with, where many learners have submitted their code and documented their approach.
The success of AlphaGo and its use of reinforcement learning has prompted interest in this method. Combined with deep learning, reinforcement learning has become a powerful tool for many applications. The time of reinforcement learning has come!
