176. x = –1
First, add 3 to each side of the equation.
![]()
Now raise each side of the equation to the third power.
4 – 4x = x 3 + 9x 2 + 27x + 27
Set the equation equal to 0 and solve for x.
0 = x 3 + 9x 2 + 31x + 23
You can use synthetic division to find a solution/factor; try x = –1.
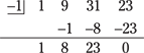
x = –1 is a solution, so x + 1 is a factor of the polynomial. You can write x 3 + 9x 2 + 31x + 23 as (x + 1)(x 2 + 8x + 23), using the coefficients in the bottom row of the synthetic division.
The quadratic doesn’t factor, and, using the quadratic formula, you get imaginary
numbers. The imaginary/complex answers are ![]() .
.
So the only possible real answer is x = –1.
Check x = –1 using the original equation.
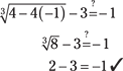
So the solution x = –1 works.
177. x = 13
Square both sides of the equation.
![]()
Now add –5 to both sides.
![]()
Square both sides again.
x + 3 = 16
Solve for x.
x = 13
Check x = 13 in the ...

