A First Course in Mathematical Logic and Set Theory

CHAPTER 7

MODELS

7.1 FIRST-ORDER SEMANTICS

We now return to logic. In Section 1.5, we proved that propositional logic is both sound and complete (Theorems 1.5.9 and 1.5.15). We now do the same for first-order logic. We have an added complication in that this logic involves formulas with variables. Sometimes the variables are all bound resulting in a sentence (Definition 2.2.14), but other times the formula will have free occurrences. We need additional machinery to handle this. Throughout this chapter, let A be a first-order alphabet and S its set of theory symbols. We start with the fundamental definition (compare Definition 4.1.1).

DEFINITION 7.1.1

The pair = (A, ) is an S-structure if A ≠ ∅ and is a function with domain S such that

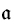• (c) is an element of A for every constant c ∈ S,
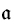• (R) is an n-ary relation on A for every n-ary relation symbol R ∈ S,
• (f) is an n-ary function on A for ...