0
INNER PRODUCT SPACES
0.1 MOTIVATION
For two vectors X = (x1, x2, x3), Y = (y1, y2, y3) in R3, the standard (Euclidean) inner product of X and Y is defined as
![]()
This definition is partly motivated by the desire to measure the length of a vector, which is given by the Pythagorean Theorem:
![]()
The goal of this chapter is to define the concept of an inner product in a more general setting that includes a wide variety of vector spaces. We are especially interested in the inner product defined on vector spaces whose elements are signals (i.e., functions of time).
0.2 DEFINITION OF INNER PRODUCT
The definition of an inner product in R3 naturally generalizes to Rn for any dimension n. For two vectors X = (x1, x2, …, xn), Y = (y1, y2,… , yn) in Rn, the Euclidean inner product is
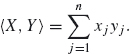
When we study Fourier series and the Fourier transform, we will use the complex exponential. Thus, we must consider complex vector spaces as well as real ones. The preceding definition can be modified for vectors in Cn by conjugating the second factor. Recall that the conjugate of a complex number z = x + iy is defined as Note that which by definition is |z|2 [the square of the length of z = x + iy regarded as a vector ...

