A First Course in Applied Mathematics

CHAPTER 1

BASICS OF LINEAR ALGEBRA

Undoubtedly, one of the subjects in mathematics that has become more indispensable than ever is linear algebra. Several application problems involve at some stage solving linear systems, the computation of eigenvalues and eigenvectors, linear transformations, bases of vector subspaces, and matrix factorizations, to mention a few. One very important characteristic of linear algebra is that as a first course, it requires only very basic pre-requisites so that it can be taught very early at undergraduate level; at the same time, mastering vector spaces, linear transformations and their natural extensions to function spaces is essential for researchers in any area of applied mathematics. Linear algebra has innumerable applications, including differential equations, least-square solutions and optimization, demography, electrical engineering, fractal geometry, communication networks, compression, search engines, social sciences, etc. In the next sections we briefly review the concepts of linear algebra that we will need later on.

1.1 NOTATION AND TERMINOLOGY

We start this section by defining an m × n matrix as a rectangular array of elements arranged in m rows and n columns, and we say the matrix is of order m × n. We usually denote the elements of a matrix A of order m × n as a_ij, where i = 1,… m, j = 1,…, n, and we write the matrix A as

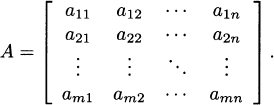
Although the ...