8.6 Illustrative example
This example is to display the fact that the initial conditions of βNH(t) and u(t) must satisfy some conditions in order that the system is impulsive free and the fact that the proposed approach is efficient in analyzing the impulsive property of the system.
Consider the following LNHMDE:
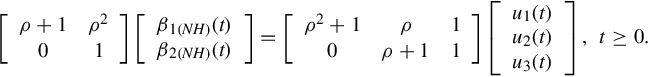 (8.32)
(8.32)
with the initial values
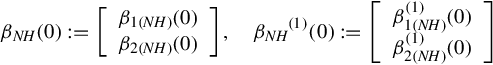
and
we have
Get A Generalized Framework of Linear Multivariable Control now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

