A Modern Theory of Random Variation: With Applications in Stochastic Calculus, Financial Mathematics, and Feynman Integration

Chapter 4

Theory of the Integral

In this chapter, using Definition 15 of the Burkill-complete integral in Chapter 3, theorems needed for study of random variability are stated and proved. The basic features and structure of the Henstock integral have been introduced in preceding chapters and are formally presented here.

4.1   The Henstock Integral

A system, called a division system¹ is posited, with the following components and relationships.

• There is a domain W, consisting of points x, with a class I(W) of subsets, called cells of W. The domain W belongs to I(W).
• The union E of a finite number of cells I is called a figure. The class of figures in W is denoted by E(W).
• A finite collection of disjoint cells I whose union is E is called a partition of E (often denoted ).

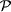DS1 Association Axiom: For each I I(W) there is a class of points I*, and if x I* the pair (x, I) are said to be associated.

• Equivalently, for each x W* there is a class x* of cells I, and if I x* the pair (x, I