A Modern Theory of Random Variation: With Applications in Stochastic Calculus, Financial Mathematics, and Feynman Integration

Chapter 5

Random Variability

Suppose T is a finite or infinite labeling set. For the purposes of this book the domain R^T is structured by means of a number of features:

• points x = x_T;
• cells I = I[N] I(R^T);
• figures E E(R^T);
• point-cell association x I[N]* and I[N] x*;
• partitions 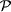, divisions , gauges γ;
• integral h, and variation V_h, defined for functions h(x, N, I) of associated triples (x, N, I[N]).

A real- or complex-valued function F defined on the figures E(R^T) of R^T is an additive (or Stieltjes) cell function if F is finitely additive on disjoint figures. A Stieltjes cell function F is a distribution function or potentiality distribution function if F(R^T) = 1. Every Stieltjes cell function is integrable (in the Stieltjes-complete or Henstock sense) on figures.

If an experiment (measurement ...