Chapter 6
Gaussian Integrals
This chapter deals with properties of exponential functions which are density functions for the distribution functions of important classes of observables. (Density function is a point function for which the distribution function is the Riemann-complete indefinite integral.)
6.1 Fresnel’s Integral
The integrals
![]()
are well known in their familiar notation,
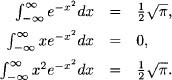
The latter integrals exist as improper or extended Riemann integrals. The familiar proof of the first one runs as follows.
Lemma 10
![]()
Proof. Let ρ > 0 and let
![]()
By Theorem 46 (integration by substitution), the Riemann integral
![]()
can be evaluated using polar co-ordinates (r, θ):
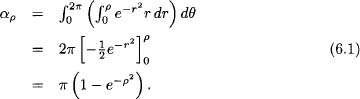
Letting ρ → ∞,
![]()
For λ = 1,2,3,… let Jλ = [−λ, λ] × [−λ, λ]. Then
If equation (6.2) is correct, it implies that βλ converges as λ → ∞, ...
Get A Modern Theory of Random Variation: With Applications in Stochastic Calculus, Financial Mathematics, and Feynman Integration now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

