A Signal Theoretic Introduction to Random Processes

14 THE FIRST PASSAGE TIME

14.1 INTRODUCTION

For signals defined by a random process X(Ω, t) on an interval [0,T], the characteristics, illustrated in Figure 14.1, can be defined and, in an appropriate context, provide valuable information. These characteristics include the maximum and minimum level; the first passage time to, or first level crossing time of, a set level; the time spent above a set level; the number of level crossings of a set level; the signal path length; etc.

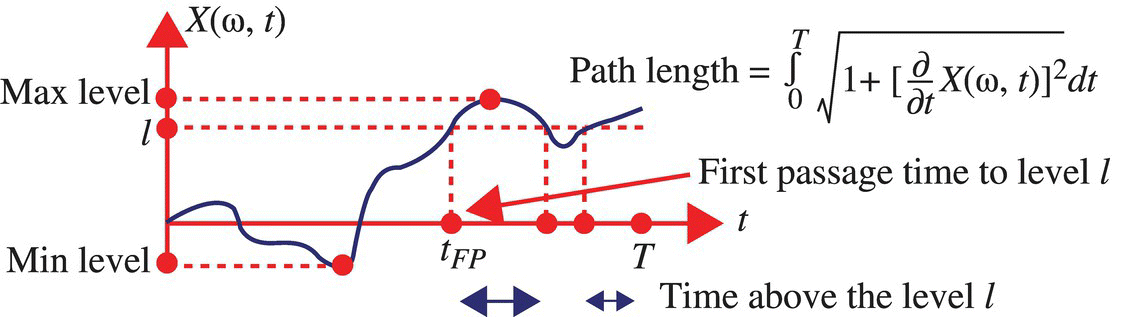
Figure 14.1 Illustration of one signal, X(ω, t), from the random process X(Ω, t) and associated characteristics.

This chapter provides an introduction to first passage time theory. In general, useful ways of characterizing the first passage time for signals defined by a random process are analytically difficult with results obtainable for a few important cases including the random walk, one-dimensional Brownian motion, monotonically increasing signals, and the linear signal plus noise case under limiting, but useful, conditions. These cases are considered along with general approaches including a Rice series approach and an integral equation approach. Finally, the relationship for a random process, between the maximum level on an interval and the first passage time on the same interval, is defined.

14.2 FIRST PASSAGE TIME

When the system performance, in some manner, is affected by a system ...