A Workout in Computational Finance

5 Upwinding Techniques for Short Rate Models

5.1 DERIVATION OF A PDE FOR SHORT RATE MODELS

Assume the short rate r_t (see Chapter 4) is modeled by an Itô process,

dr_t = μ(r, t)dt + σ(r, t)dW_t,

where we again use the notation r(t) = r_t, W_t is a Brownian motion, and μ and σ are functions to be defined later.

We are interested in the change dV of the value of an interest rate instrument V(r_t, t) in an infinitesimally short time interval dt. Again, we utilize Itô’s Lemma and try to use the same kind of analysis that has been successful in deriving the Black-Scholes PDE (PS-PDE), where we got rid of the stochastic terms in the BS-PDE by Δ-hedging.

We set up a self-replicating portfolio π containing two interest rate instruments¹ with different maturities T₁ and T₂ and corresponding values V₁ and V₂ (Hull, 2002). By applying the Itô Lemma for an infinitesimal change dπ_t = dV₁ − ΔdV₂, we obtain

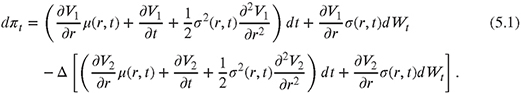
Choosing, the stochastic terms in the equation above can be eliminated. To avoid arbitrage, we have to use the risk-free rate,

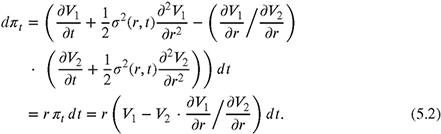
Rearranging equations (5.3)-(5.5) yields

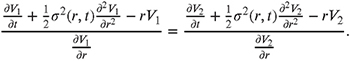
This equality only holds when ...