Advanced Analytics with Spark

Chapter 4. Predicting Forest Cover with Decision Trees

Sean Owen

Prediction is very difficult, especially if it’s about the future.

Niels Bohr

In the late 19th century, the English scientist Sir Francis Galton was busy measuring things like peas and people. He found that large peas (and people) had larger-than-average offspring. This isn’t surprising. However, the offspring were, on average, smaller than their parents. In terms of people: the child of a 7-foot-tall basketball player is likely to be taller than the global average, but still more likely than not to be less than 7 feet tall.

As almost a side effect of his study, Galton plotted child versus parent size and noticed there was a roughly linear relationship between the two. Large parent peas had large children, but slightly smaller than themselves; small parents had small children, but generally a bit larger than themselves. The line’s slope was therefore positive but less than 1, and Galton described this phenomenon as we do today, as regression to the mean.

Although maybe not perceived this way at the time, this line was, to me, an early example of a predictive model. The line links the two values, and implies that the value of one suggests a lot about the value of the other. Given the size of a new pea, this relationship could lead to a more accurate estimate of its offsprings’ size than simply assuming the offspring would be like the parent or like every other pea.

Fast Forward to Regression

More than a century of statistics later, and since the advent of modern machine learning and data science, we still talk about the idea of predicting a value from other values as regression, even though it has nothing to do with slipping back toward a mean value, or indeed moving backward at all. Regression techniques also relate to classification techniques. Generally, regression refers to predicting a numeric quantity like size or income or temperature, while classification refers to predicting a label or category, like “spam” or “picture of a cat.”

The common thread linking regression and classification is that both involve predicting one (or more) values given one (or more) other values. To do so, both require a body of inputs and outputs to learn from. They need to be fed both questions and known answers. For this reason they are known as types of supervised learning.

Classification and regression are the oldest and most well-studied types of predictive analytics. Most algorithms you will likely encounter in analytics packages and libraries are classification or regression techniques, like support vector machines, logistic regression, naïve Bayes, neural networks, and deep learning. Recommenders, the topic of Chapter 3, were comparatively more intuitive to introduce, but are also just a relatively recent and separate subtopic within machine learning.

This chapter will focus on a popular and flexible type of algorithm for both classification and regression: decision trees, and its extension, random decision forests. The exciting thing about these algorithms is that, with respect to Mr. Bohr, they can help predict the future—or at least, predict the things we don’t yet know for sure, like your likelihood to buy a car based on your online behavior, whether an email is spam given its words, or which acres of land are likely to grow the most crops given their location and soil chemistry.

Vectors and Features

To explain the choice of the data set and algorithm featured in this chapter, and to begin to explain how regression and classification operate, it is necessary to briefly define the terms that describe their input and output.

Consider predicting tomorrow’s high temperature given today’s weather. There is nothing wrong with this idea, but “today’s weather” is a casual concept, and requires structuring before it can be fed into a learning algorithm.

It is really certain features of today’s weather that may predict tomorrow’s temperature, such as:

• Today’s high temperature

• Today’s low temperature

• Today’s average humidity

• Whether it’s cloudy, rainy, or clear today

• The number of weather forecasters predicting a cold snap tomorrow

These features are also sometimes called dimensions, predictors, or just variables. Each of these features can be quantified. For example, high and low temperatures are measured in degrees Celsius, humidity can be measured as a fraction between 0 and 1, and weather type can be labeled cloudy, rainy, or clear. The number of forecasters is, of course, an integer count. Today’s weather might therefore be reduced to a list of values like 13.1,19.0,0.73,cloudy,1.

These five features together, in order, are known as a feature vector, and can describe any day’s weather. This usage bears some resemblance to use of the term vector in linear algebra, except that a vector in this sense can conceptually contain nonnumeric values, and even lack some values.

These features are not all of the same type. The first two features are measured in degrees Celsius, but the third is unitless, a fraction. The fourth is not a number at all, and the fifth is a number that is always a nonnegative integer.

For purposes of discussion, this book will talk about features in two broad groups only: categorical features and numeric features. Numeric features, here, are those that can be quantified by a number and have a meaningful ordering. For example, it’s meaningful to say that today’s high was 23C, and that this is larger than yesterday’s high of 22C. All of the features mentioned previously are numeric, except the weather type. Terms like clear are not numbers, and have no ordering. It is meaningless to say that cloudy is larger than clear. This is a categorical feature, which instead takes on one of several discrete values.

Training Examples

A learning algorithm needs to train on data in order to make predictions. It requires a large number of inputs, and known correct outputs, from historical data. For example, in this problem, the learning algorithm would be given that, one day, the weather was between 12 and 16 degrees Celsius, with 10% humidity, clear, with no forecast of a cold snap, and the following day, the high temperature was 17.2 degrees. With enough of these examples, a learning algorithm might learn to predict the following day’s high temperature with some accuracy.

Feature vectors provide an organized way to describe input to a learning algorithm (here: 12.5,15.5,0.10,clear,0). The output, or target, of the prediction can also be thought of as a feature, here a numeric feature: 17.2.

It’s not uncommon to simply include the target as another feature in the feature vector. The entire training example might be thought of as 12.5,15.5,0.10,clear,0,17.2. The collection of all of these examples is known as the training set.

Note that regression problems are just those where the target is a numeric feature, and classification problems are those where the target is categorical. Not every regression or classification algorithm can handle categorical features, or categorical targets; some are limited to numeric features.

Decision Trees and Forests

It turns out that the family of algorithms known as decision trees can naturally handle both categorical and numeric features. They can be built in parallel easily. They are robust to outliers in the data, meaning that a few extreme and possibly erroneous data points may not affect predictions at all. They can consume data of different types and on different scales without the need for preprocessing or normalization, which is an issue that will reappear in Chapter 5.

Decision trees generalize into a more powerful algorithm, called random decision forests. Their flexibility makes these algorithms worthwhile to examine in this chapter, where Spark MLlib’s DecisionTree and RandomForest implementation will be applied to a data set.

Decision tree–based algorithms have the further advantage of being comparatively intuitive to understand and reason about. In fact, we all probably use the same reasoning embodied in decision trees, implicitly, in everyday life. For example, I sit down to have morning coffee with milk. Before I commit to that milk and add it to my brew, I want to predict: is the milk spoiled? I don’t know for sure. I might check if the use-by date has passed. If not, I predict no, it’s not spoiled. If the date has passed, but that was three or fewer days ago, I take my chances and predict no, it’s not spoiled. Otherwise, I sniff the milk. If it smells funny, I predict yes, and otherwise no.

This series of yes/no decisions that lead to a prediction are what decision trees embody. Each decision leads to one of two results, which is either a prediction or another decision, as shown in Figure 4-1. In this sense, it is natural to think of the process as a tree of decisions, where each internal node in the tree is a decision, and each leaf node is a final answer.

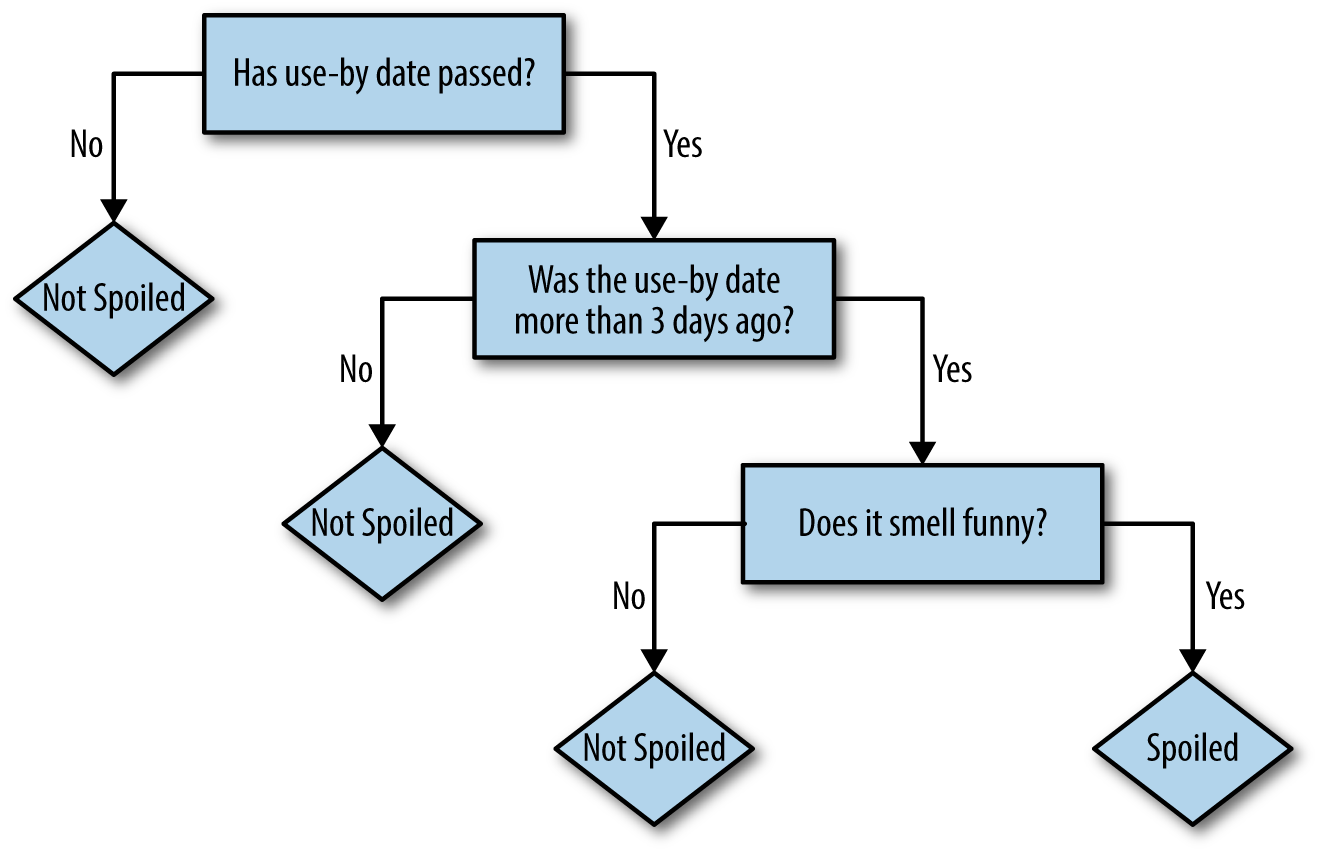
Figure 4-1. Decision tree: Is it spoiled?

The preceding rules were ones I learned to apply intuitively over years of bachelor life—they seemed like rules that were both simple and also usefully differentiated cases of spoiled and nonspoiled milk. These are also properties of a good decision tree.

That is a simplistic decision tree, and was not built with any rigor. To elaborate, consider another example. A robot has taken a job in an exotic pet store. It wants to learn, before the shop opens, which animals in the shop would make a good pet for a child. The owner lists nine pets that would and wouldn’t be suitable before hurrying off. The robot compiles the information found in Table 4-1 from examining the animals.

Table 4-1. Exotic pet store “feature vectors”

Name	Weight (kg)	# Legs	Color	Good pet?
Fido	20.5	4	Brown	Yes
Mr. Slither	3.1	0	Green	No
Nemo	0.2	0	Tan	Yes
Dumbo	1390.8	4	Grey	No
Kitty	12.1	4	Grey	Yes
Jim	150.9	2	Tan	No
Millie	0.1	100	Brown	No
McPigeon	1.0	2	Grey	No
Spot	10.0	4	Brown	Yes

Although a name is given, it will not be included as a feature. There is little reason to believe the name alone is predictive; “Felix” could name a cat or a poisonous tarantula, for all the robot knows. So, there are two numeric features (weight, number of legs) and one categorical feature (color) predicting a categorical target (is/is not a good pet for a child).

The robot might try to fit a simple decision tree to this training data to start, consisting of a single decision based on weight, as shown in Figure 4-2.

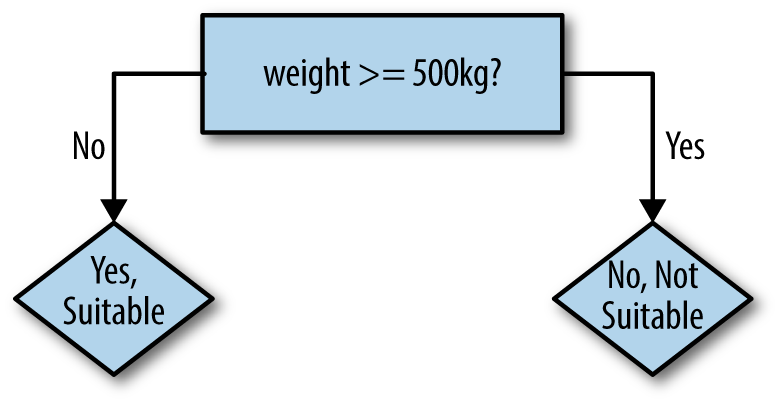
Figure 4-2. Robot’s first decision tree

The logic of the decision tree is easy to read and make some sense of: 500kg animals certainly sound unsuitable as pets. This rule predicts the correct value in five of nine cases. A quick glance suggests that we could improve the rule by lowering the weight threshold to 100kg. This gets six of nine examples correct. The heavy animals are now predicted correctly; the lighter animals are only partly correct.

So, a second decision can be constructed to further refine the prediction for examples with weights less than 100kg. It would be good to pick a feature that changes some of the incorrect Yes predictions to No. For example, there is one small green animal, sounding suspiciously like a snake, that the robot could predict correctly by deciding on color, as in Figure 4-3.

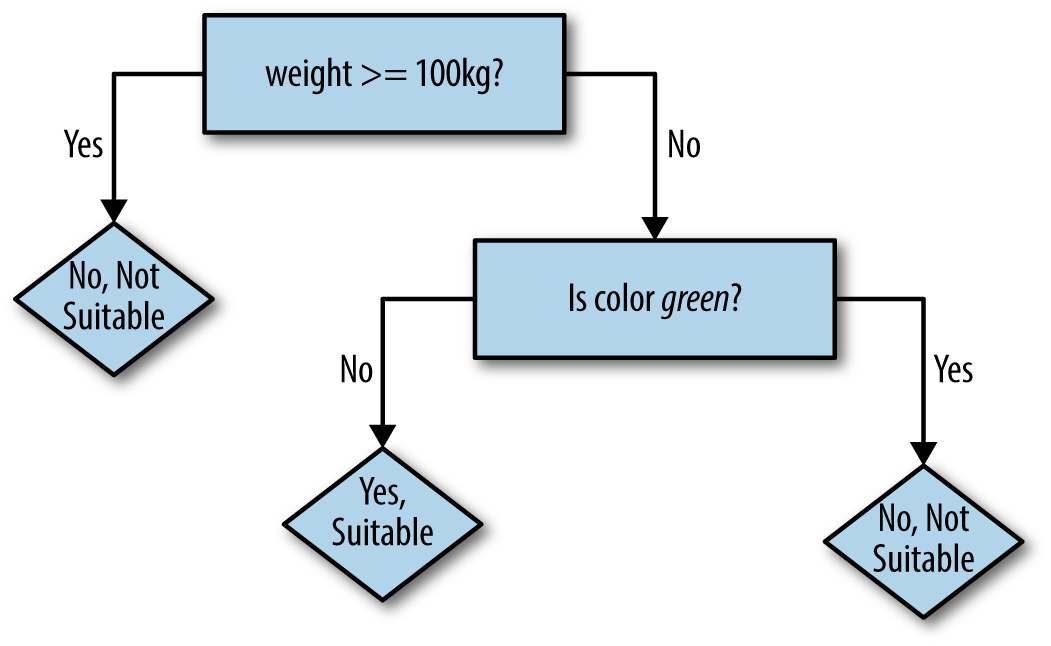
Figure 4-3. Robot’s next decision tree

Now, seven of nine examples are correct. Of course, decision rules could be added until all nine were correctly predicted. The logic embodied in the resulting decision tree would probably sound implausible when translated into common speech: “If the animal’s weight is less than 100kg, and its color is brown instead of green, and it has fewer than 10 legs, then yes it is a suitable pet.” While perfectly fitting the given examples, a decision tree like this would fail to predict that a small, brown, four-legged wolverine is not a suitable pet. Some balance is needed to avoid this phenomenon, known as overfitting.

This is enough of an introduction to decision trees for us to begin using them with Spark. The remainder of the chapter will explore how to pick decision rules, how to know when to stop, and how to gain accuracy by creating a forest of trees.

Covtype Data Set

The data set used in this chapter is the well-known Covtype data set, available online as a compressed CSV-format data file, covtype.data.gz, and accompanying info file, covtype.info.

The data set records the types of forest covering parcels of land in Colorado, USA. It’s only coincidence that the data set concerns real-world forests! Each example contains several features describing each parcel of land, like its elevation, slope, distance to water, shade, and soil type, along with the known forest type covering the land. The forest cover type is to be predicted from the rest of the features, of which there are 54 in total.

This data set has been used in research, and even a Kaggle competition. It is an interesting data set to explore in this chapter because it contains both categorical and numeric features. There are 581,012 examples in the data set, which does not exactly qualify as big data, but is large enough to be manageable as an example and still highlight some issues of scale.

Preparing the Data

Thankfully, the data is already in a simple CSV format and does not require much cleansing or other preparation to be used with Spark MLlib. Later, it will be of interest to explore some transformations of the data, but it can be used as is to start.

The covtype.data file should be extracted and copied into HDFS. This chapter will assume that the file is available at /user/ds/. Start spark-shell.

The Spark MLlib abstraction for a feature vector is known as a LabeledPoint, which consists of a Spark MLlib Vector of features, and a target value, here called the label. The target is a Double value, and Vector is essentially an abstraction on top of many Double values. This suggests that LabeledPoint is only for numeric features. It can be used with categorical features, with appropriate encoding.

One such encoding is one-hot or 1-of-n encoding, in which one categorical feature that takes on N distinct values becomes N numeric features, each taking on the value 0 or 1. Exactly one of the N values has value 1, and the others are 0. For example, a categorical feature for weather that can be cloudy, rainy, or clear would become three numeric features, where cloudy is represented by 1,0,0; rainy by 0,1,0; and so on. These three numeric features might be thought of as is_cloudy, is_rainy, and is_clear features.

Another possible encoding simply assigns a distinct numeric value to each possible value of the categorical feature. For example, cloudy may become 1.0, rainy 2.0, and so on.

Be careful when encoding a categorical feature as a single numeric feature. The original categorical values have no ordering, but when encoded as a number, they appear to. Treating the encoded feature as numeric leads to meaningless results because the algorithm is effectively pretending that rainy is somehow greater than, and two times larger than, cloudy. It’s OK as long as the encoding’s numeric value is not used as a number.

All of the columns contain numbers, but the Covtype data set does not consist solely of numeric features, at heart. The covtype.info file says that four of the columns are actually a one-hot encoding of a single categorical feature, called Wilderness_Type, with four values. Likewise, 40 of the columns are really one Soil_Type categorical feature. The target itself is a categorical value encoded as the values 1 to 7. The remaining features are numeric features in various units, like meters, degrees, or a qualitative “index” value.

We see both types of encodings of categorical features, then. It would have, perhaps, been simpler and more straightforward to not encode such features (and in two ways, no less), and instead simply include their values directly like “Rawah Wilderness Area.” This may be an artifact of history; the data set was released in 1998. For performance reasons, or to match the format expected by libraries of the day, which were built more for regression problems, data sets often contain data encoded in these ways.

A First Decision Tree

To start, the data will be used as is. The DecisionTree implementation, like several in Spark MLlib, requires input in the form of LabeledPoint objects:

import org.apache.spark.mllib.linalg._
import org.apache.spark.mllib.regression._

val rawData = sc.textFile("hdfs:///user/ds/covtype.data")

val data = rawData.map { line =>
  val values = line.split(',').map(_.toDouble)
  val featureVector = Vectors.dense(values.init) 
  val label = values.last - 1 
  LabeledPoint(label, featureVector)
}

init returns all but last value; target is last column

DecisionTree needs labels starting at 0; subtract 1

In Chapter 3, we built a recommender model right away on all of the available data. This created a recommender that could be sense-checked by anyone with some knowledge of music: looking at a user’s listening habits and recommendations, we got some sense that it was producing good results. Here, that is not possible. We would have no idea how to make up a new 54-feature description of a new parcel of land in Colorado, or what kind of forest cover to expect from such a parcel.

Instead, we must jump straight to holding out some data for purposes of evaluating the resulting model. Before, the AUC metric was used to assess the agreement between held-out listening data and predictions from recommendations. The principle is the same here, although the evaluation metric will be different: precision. This time, the data will be split into the full three subsets: training, cross-validation (CV), and test. As you can see, 80% of the data is used for training, and 10% each for cross-validation and test:

val Array(trainData, cvData, testData) =
  data.randomSplit(Array(0.8, 0.1, 0.1))
trainData.cache()
cvData.cache()
testData.cache()

As with the ALS implementation, the DecisionTree implementation has several hyperparameters for which a value must be chosen. So, as before, the training and CV sets are used to choose a good setting of these hyperparameters for this data set. Here, the third set, the test set, is then used to produce an unbiased evaluation of the expected accuracy of a model built with those hyperparameters. The accuracy of the model on just the cross-validation set tends to be biased and slightly too optimistic. This chapter will take this extra step of evaluating the final model on the test set.

But first, try building a DecisionTreeModel on the training set, with some default arguments, and compute some metrics about the resulting model using the CV set:

import org.apache.spark.mllib.evaluation._
import org.apache.spark.mllib.tree._
import org.apache.spark.mllib.tree.model._
import org.apache.spark.rdd._

def getMetrics(model: DecisionTreeModel, data: RDD[LabeledPoint]):
    MulticlassMetrics = {
  val predictionsAndLabels = data.map(example =>
    (model.predict(example.features), example.label)
  )
  new MulticlassMetrics(predictionsAndLabels)
}

val model = DecisionTree.trainClassifier(
  trainData, 7, Map[Int,Int](), "gini", 4, 100)

val metrics = getMetrics(model, cvData)

Here, the use of trainClassifier instead of trainRegressor suggests that the target value within each LabeledPoint should be treated as a distinct category number, not a numeric feature value. (trainRegressor works similarly for regression problems, and will not be discussed separately in this chapter.)

At this time, we must specify the number of target values it will encounter: 7. The Map holds information about categorical features; this will be discussed later along with the meaning of “gini,” the maximum depth of 4, and the maximum bin count of 100.

MulticlassMetrics computes standard metrics that in different ways measure the quality of the predictions from a classifier, which here has been run on the CV set. Ideally, the classifier should predict the correct target category for each example in the CV set. The metrics available here measure this sort of correctness, in different ways.

Its companion class, BinaryClassificationMetrics, contains similar evaluation metric implementations for the particular, common case of a categorical target with just two values. It can’t be used directly here because the target takes on many values.

It may be helpful to look at the confusion matrix first:

metrics.confusionMatrix

...
14019.0  6630.0   15.0    0.0    0.0  1.0   391.0
5413.0   22399.0  438.0   16.0   0.0  3.0   50.0
0.0      457.0    2999.0  73.0   0.0  12.0  0.0
0.0      1.0      163.0   117.0  0.0  0.0   0.0
0.0      872.0    40.0    0.0    0.0  0.0   0.0
0.0      500.0    1138.0  36.0   0.0  48.0  0.0
1091.0   41.0     0.0     0.0    0.0  0.0   891.0

Your values will be a little different. The process of building a decision tree includes some random choices that can lead to slightly different classifications.

Because there are seven target category values, this is a 7-×-7 matrix, where each row corresponds to an actual correct value, and each column to a predicted value, in order. The entry at row i and column j counts the number of times an example with true category i was predicted as category j. So, the correct predictions are the counts along the diagonal, and incorrect predictions are everything else. Counts are high along the diagonal, which is good. However, there are certainly a number of misclassifications, and, for example, category 5 is never predicted at all.

It’s helpful to summarize the accuracy with a single number. An obvious place to start is to compute the fraction of all examples that were correctly predicted:

metrics.precision

...
0.7030630195577938

About 70% of examples were classified correctly. This is commonly called accuracy, and is called precision in Spark’s MulticlassMetrics. This is a light overloading of the term.

Precision is actually a common metric for binary classification problems, where there are two category values, not several. In a binary classification problem, where there is some kind of positive and negative class, precision is the fraction of examples that the classifier marked positive that are actually positive. It is often accompanied by the metric recall. This is the fraction of all examples that are actually positive that the classifier marked positive.

For example, say there are 20 actually positive examples in a data set of 50 examples. The classifier marks 10 of the 50 as positive, and of those 10, 4 are actually positive (correctly classified). Precision is 4/10 = 0.4 and recall is 4/20 = 0.2 in this case.

We can apply these concepts to this multiclass problem by viewing each category independently as the positive class, and all else as negative. For example, to compute precision and recall for each category versus the rest:

(0 until 7).map( 
  cat => (metrics.precision(cat), metrics.recall(cat))
).foreach(println)

...
(0.6805931840866961,0.6809492105763744)
(0.7297560975609756,0.7892237892589596)
(0.6376224968044312,0.8473952434881087)
(0.5384615384615384,0.3917910447761194)
(0.0,0.0)
(0.7083333333333334,0.0293778801843318)
(0.6956168831168831,0.42828585707146427)

DecisionTreeModel numbers categories from 0

This shows that the accuracy for each class individually varies. For our purposes here, there’s no reason to think that one category’s accuracy is more important than another, so examples will take the overall multiclass precision as a good, single measure of the accuracy of predictions.

Although 70% accuracy sounds decent, it’s not immediately clear whether it is outstanding or poor. How well would a simplistic approach do, to establish a baseline? Just as a broken clock is correct twice a day, randomly guessing a classification for each example would also occasionally produce the correct answer.

We could construct such a “classifier” by picking a class at random in proportion to its prevalence in the training set. Each classification would be correct in proportion to its prevalence in the CV set. For example, a class that makes up 20% of the training set and 10% of the CV set will contribute 20% of 10%, or 2%, to the overall accuracy. That 10% will be correctly “classified” 20% of the time through guessing. We can evaluate the accuracy by summing these products of probabilities:

import org.apache.spark.rdd._

def classProbabilities(data: RDD[LabeledPoint]): Array[Double] = {
  val countsByCategory = data.map(_.label).countByValue() 
  val counts = countsByCategory.toArray.sortBy(_._1).map(_._2) 
  counts.map(_.toDouble / counts.sum)
}

val trainPriorProbabilities = classProbabilities(trainData)
val cvPriorProbabilities = classProbabilities(cvData)
trainPriorProbabilities.zip(cvPriorProbabilities).map { 
  case (trainProb, cvProb) => trainProb * cvProb
}.sum

...
0.37737764750734776

Count (category,count) in data

Order counts by category and extract counts

Pair probability in training, CV set and sum products

Random guessing achieves 37% accuracy then, which makes 70% seem like a good result after all. But this result was achieved with default arguments to DecisionTree.trainClassifier(). We can do even better by exploring what these arguments—hyperparameters—mean for the tree-building process.

Decision Tree Hyperparameters

In Chapter 3, the ALS algorithm exposed several hyperparameters whose values we had to choose by building models with various combinations of values, and then assessing the quality of each result using some metric. The process is the same here, although the metric is now multiclass accuracy instead of AUC, and the hyperparameters controlling how the tree’s decisions are chosen are maximum depth, maximum bins, and impurity measure.

Maximum depth simply limits the number of levels in the decision tree. It is the maximum number of chained decisions that the classifier will make to classify an example. It is useful to limit this to avoid overfitting the training data, as illustrated previously in the pet store example.

The decision tree algorithm is responsible for coming up with potential decision rules to try at each level, like the weight >= 100 or weight >= 500 decisions in the pet store example. Decisions are always of the same form: for numeric features, decisions are of the form feature >= value, and for categorical features they are of the form feature in (value1, value2, …). So, the set of decision rules to try is really a set of values to plug in to the decision rule. These are referred to as “bins” in the Spark MLlib implementation. A larger number of bins requires more processing time but may lead to finding a more optimal decision rule.

What makes a decision rule good? Intuitively, a good rule would meaningfully distinguish examples by target category value. For example, a rule that divides the Covtype data set into examples with only categories 1–3 on the one hand, and 4–7 on the other, would be excellent because it clearly separates some categories from the others. A rule that resulted in about the same mix of all categories as are found in the whole data set doesn’t seem helpful. Following either branch of such a decision leads to about the same distribution of possible target values, and so doesn’t really make progress toward a confident classification.

Put another way, good rules divide the training data’s target values into relatively homogeneous, or “pure,” subsets. Picking a best rule means minimizing the impurity of the two subsets it induces. There are two commonly used measures of impurity: Gini impurity and entropy.

Gini impurity is directly related to the accuracy of the random-guess classifier. Within a subset, it is the probability that a randomly chosen classification of a randomly chosen example (both according to the distribution of classes in the subset) is incorrect. This is the sum of products of proportions of classes, but with themselves, and subtracted from 1. If a subset has N classes and p_i is the proportion of examples of class i, then its Gini impurity is given in the Gini impurity equation:

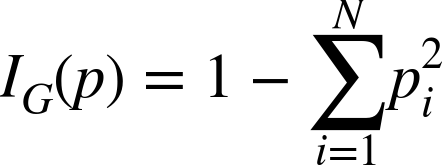
If the subset contains only one class, this value is 0 because it is completely “pure.” When there are N classes in the subset, this value is larger than 0 and is largest when the classes occur the same number of times—maximally impure.

Entropy is another measure of impurity, borrowed from information theory. Its nature is more difficult to explain, but it captures how much uncertainty the collection of target values in the subset contains. A subset containing one class only is completely certain, and has 0 entropy. Hence low entropy, like low Gini impurity, is a good thing. Entropy is defined in the entropy equation:

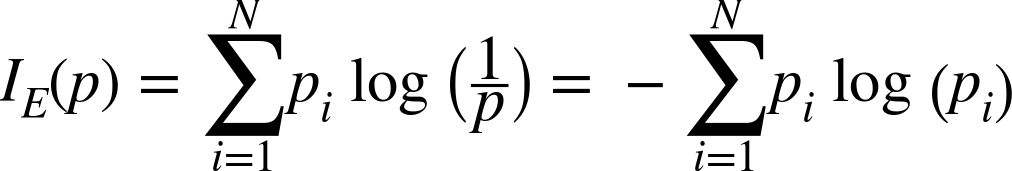
Interestingly, uncertainty has units. Because the logarithm is the natural log (base e), the units are nats, the base-e counterpart to more familiar bits (which we can obtain by using log base 2 instead). It really is measuring information, and so it’s also common to talk about the information gain of a decision rule when using entropy with decision trees.

One or the other measure may be a better metric for picking decision rules in a given data set. The default in Spark’s implementation is Gini impurity.

Some decision tree implementations will impose a minimum information gain, or decrease in impurity, for candidate decision rules. Rules that do not improve the subsets impurity enough are rejected. Like a lower maximum depth, this can help the model resist overfitting, because decisions that barely help divide the training input may in fact not helpfully divide future data at all. However, rules like minimum information gain are not implemented in Spark MLlib yet.

Tuning Decision Trees

It’s not obvious from looking at the data which impurity measure leads to better accuracy, or what maximum depth or number of bins is enough without being excessive. Fortunately, as in Chapter 3, it’s simple to let Spark try a number of combinations of these values and report the results:

val evaluations =
  for (impurity <- Array("gini", "entropy");
       depth    <- Array(1, 20);
       bins     <- Array(10, 300)) 
    yield {
      val model = DecisionTree.trainClassifier(
        trainData, 7, Map[Int,Int](), impurity, depth, bins)
      val predictionsAndLabels = cvData.map(example =>
        (model.predict(example.features), example.label)
      )
      val accuracy =
        new MulticlassMetrics(predictionsAndLabels).precision
      ((impurity, depth, bins), accuracy)
    }

evaluations.sortBy(_._2).reverse.foreach(println) 

...
((entropy,20,300),0.9125545571245186)
((gini,20,300),0.9042533162173727)
((gini,20,10),0.8854428754813863)
((entropy,20,10),0.8848951647411211)
((gini,1,300),0.6358065896448438)
((gini,1,10),0.6355669661959777)
((entropy,1,300),0.4861446298673513)
((entropy,1,10),0.4861446298673513)

Again, read as a triply nested for loop

Sort by second value (accuracy), descending, and print

Clearly, maximum depth 1 is too small and produces inferior results. More bins helps a little. The two impurity measures seem comparable, for reasonable settings of maximum depth. This process could be continued to explore these hyperparameters. More bins should never hurt, but will slow down the building process and increase memory usage. Both impurity measures should be tried in all cases. More depth will help up to a point.

So far, the code samples here have ignored the 10% of data held out as the test set. If the purpose of the CV set was to evaluate parameters fit to the training set, then the purpose of the test set is to evaluate hyperparameters that were “fit” to the CV set. That is, the test set ensures an unbiased estimate of the accuracy of the final, chosen model and its hyperparameters.

The preceding test suggests that entropy-based impurity, maximum depth 20, and 300 bins are the best-known hyperparameter settings so far, and achieves about 91.2% accuracy. However, there’s an element of randomness in how these models are built. By chance, this model and evaluation could have turned out unusually well. The top model and evaluation result could have benefited from a bit of luck, and so, its accuracy estimate is likely to be slightly optimistic. Put another way, hyperparameters can overfit too.

To really assess how well this best model is likely to perform on future examples, we need to evaluate it on examples that were not used to train it, certainly. But we also need to avoid examples in the CV set that were used to evaluate it. That is why a third subset, the test set, was held out. As a final step, we can use the hyperparameters to build a model on the training and CV sets together, and evaluate as before:

val model = DecisionTree.trainClassifier(
  trainData.union(cvData), 7, Map[Int,Int](), "entropy", 20, 300)

The result is about 91.6% accuracy, which is about the same, so the initial estimate appears to have been reliable.

This is an interesting point at which to revisit the issue of overfitting. As discussed previously, it’s possible to build a decision tree so deep and elaborate that it fits the given training examples very well or perfectly, but fails to generalize to other examples because it has fit the idiosyncrasies and noise of the training data too closely. This is a problem common to most machine learning algorithms, not just decision trees.

When a decision tree has overfit, it will exhibit high accuracy when run on the same training data that it fit the model to, but low accuracy on other examples. Here, the final model’s accuracy was about 91.6% on other, new examples. Accuracy can just as easily be evaluated over the same data that the model was trained on, trainData.union(cvData). This gives an accuracy of about 95.3%.

The difference is not large, but suggests the decision tree has overfit the training data to some extent. A lower maximum depth might be a better choice.

Categorical Features Revisited

The code samples so far have included the argument Map[Int,Int]() without explanation. This parameter, like the 7, specifies the number of distinct values to expect for each categorical feature in the input. The keys in this Map are indices of features in the input Vector, and values are distinct value counts. At this time, the implementation requires this information in advance.

The empty Map() indicates that no features should be treated as categorical; all are numeric. All of the features are in fact numbers, but some represent categorical features, conceptually. As mentioned earlier, it would be an error to treat a categorical feature that had simply been mapped to distinct numbers as a numeric value, because the algorithm would be trying to learn from an ordering that has no meaning.

Thankfully, the categorical features here are one-hot encoded as several binary 0/1 values. Treating these individual features as numeric turns out to be fine, because any decision rule on the “numeric” features will choose thresholds between 0 and 1, and all are equivalent since all values are 0 or 1.

Of course, this encoding forces the decision tree algorithm to consider the values of the underlying categorical feature individually. It is not limited in this way when learning from a single categorical feature. With one 40-valued categorical feature, the decision tree can create decisions based on groups of categories in one decision, which may be more direct and optimal. On the other hand, having 40 numeric features represent one 40-valued categorical feature also increases memory usage and slows things down.

What about undoing the one-hot encoding? The following alternative parsing of the input turns the two categorical features from one-hot encoding to a series of distinct numeric values:

val data = rawData.map { line =>
  val values = line.split(',').map(_.toDouble)
  val wilderness = values.slice(10, 14).indexOf(1.0).toDouble 
  val soil = values.slice(14, 54).indexOf(1.0).toDouble 
  val featureVector =
    Vectors.dense(values.slice(0, 10) :+ wilderness :+ soil) 
  val label = values.last - 1
  LabeledPoint(label, featureVector)
}

Which of 4 “wilderness” features is 1

Similarly for following 40 “soil” features

Add derived features back to first 10

We can repeat the same process of train/CV/test split and evaluation. This time, the count of distinct values for the two new categorical features is given, which causes these features to be treated as categorical, and not numeric. DecisionTree requires the number of bins to increase to at least 40, because the soil feature has 40 distinct values. Given previous results, deeper trees are built, up to the maximum of depth 30 that DecisionTree currently supports. Finally, both train and CV accuracy are reported:

val evaluations =
  for (impurity <- Array("gini", "entropy");
       depth    <- Array(10, 20, 30);
       bins     <- Array(40, 300))
    yield {
      val model = DecisionTree.trainClassifier(
        trainData, 7, Map(10 -> 4, 11 -> 40),
        impurity, depth, bins) 
      val trainAccuracy = getMetrics(model, trainData).precision
      val cvAccuracy = getMetrics(model, cvData).precision
      ((impurity, depth, bins), (trainAccuracy, cvAccuracy)) 
    }

...
((entropy,30,300),(0.9996922984231909,0.9438383977425239))
((entropy,30,40),(0.9994469978654548,0.938934581368939))
((gini,30,300),(0.9998622874061833,0.937127912178671))
((gini,30,40),(0.9995180059216415,0.9329467634811934))
((entropy,20,40),(0.9725865867933623,0.9280773598540899))
((gini,20,300),(0.9702347139020864,0.9249630062975326))
((entropy,20,300),(0.9643948392205467,0.9231391307340239))
((gini,20,40),(0.9679344832334917,0.9223820503114354))
((gini,10,300),(0.7953203539213661,0.7946763481193434))
((gini,10,40),(0.7880624698753701,0.7860215423792973))
((entropy,10,40),(0.78206336500723,0.7814790598437661))
((entropy,10,300),(0.7821903188046547,0.7802746137169208))

Specify value count for categorical features 10, 11

Return train and CV accuracy

If you run this on a cluster, you may notice that the tree-building process completes several times faster than before.

At depth 30, the training set is fit nearly perfectly; it is overfitting to some degree, but still providing the best accuracy on the cross-validation set. Entropy, and a larger number of bins, appear to help accuracy again. The accuracy on the test set is 94.5%. By treating categorical features as actual categorical features, the classifier improved its accuracy by almost 3%.

Random Decision Forests

If you have been following along with the code examples, you may have noticed that your results differ slightly from those presented in code listings in the book. That is because there is an element of randomness in building decision trees, and the randomness comes into play when you’re deciding what data to use and what decision rules to explore.

The algorithm does not consider every possible decision rule at every level. To do so could take an incredible amount of time. For a categorical feature over N values, there are 2^N – 2 possible decision rules (every subset except the empty set and entire set). For even moderately large N this would create billions of candidate decision rules.

Instead, decision trees use several heuristics to be smarter about which few rules to actually consider. The process of picking rules also involves some randomness; only a few features picked at random are looked at each time, and only values from a random subset of the training data. This trades a bit of accuracy for a lot of speed, but it also means that the decision tree algorithm won’t build the same tree every time. This is a good thing.

It’s good for the same reason that the “wisdom of the crowds” usually beats individual predictions.

To illustrate, take this quick quiz: How many black taxis operate in London?

Don’t peek at the answer; guess first.

I guessed 10,000, which is well off the correct answer of about 19,000. Because I guessed low, you’re a bit more likely to have guessed higher than I did, and so the average of our answers will tend to be more accurate. There’s that regression to the mean again. The average guess from an informal poll of 13 people in the office was indeed closer: 11,170.

A key to this effect is that the guesses were independent and didn’t influence one another. (You didn’t peek, did you?) The exercise would be useless if we had all agreed on and used the same methodology to make a guess, because the guesses would have been the same answer—the same potentially quite wrong answer. It would even have been different and worse if I’d merely influenced you by stating my guess upfront.

It would be great to have not one tree, but many trees, each producing reasonable but different and independent estimations of the right target value. Their collective average prediction should fall close to the true answer, more than any individual tree’s does. It’s the randomness in the process of building that helps create this independence. This is the key to random decision forests.

Through RandomForest, Spark MLlib can build random decision forests, which are, as the name suggests, collections of independently built decision trees. The invocation is virtually the same:

val forest = RandomForest.trainClassifier(
  trainData, 7, Map(10 -> 4, 11 -> 40), 20,
  "auto", "entropy", 30, 300)

Two new parameters appear, compared to DecisionTree.trainClassifier(). First is a number of trees to build: here 20. This model-building process may take significantly longer than before, because 20 trees are being built instead of one.

Second is a strategy for choosing which features to evaluate at each level of the tree, which is here set to "auto". The random decision forest implementation will not even consider every feature as the basis of a decision rule, but only a subset of all features. This parameter controls how it picks the subset. Checking only a few features is of course faster, and speed is helpful now that so many more trees are being constructed.

However, it also makes the individual trees’ decisions more independent, and makes the forest as a whole less prone to overfitting. If a particular feature contains noisy data, or is deceptively predictive only in the training set, then most trees will not have considered this problem feature, most of the time. Most trees will not have fit the noise and will tend to “outvote” the ones that have in the forest.

In fact, when you’re building a random decision forest, each tree will not even necessarily see all of the training data. They may be fed a randomly chosen subset of it instead, for similar reasons.

The prediction of a random decision forest is simply a weighted average of the trees’ predictions. For a categorical target, this can be a majority vote, or the most probable value based on the average of probabilities produced by the trees. Random decision forests, like decision trees, also support regression, and the forest’s prediction in this case is the average of the number predicted by each tree.

The accuracy from this RandomForestModel model is 96.3% off the bat—about 2% better already, although viewed another way, that’s a 33% reduction in the error rate over the best decision tree built previously, from 5.5% down to 3.7%.

Random decision forests are appealing in the context of big data because trees are supposed to be built independently, and big-data technologies like Spark and MapReduce inherently need data-parallel problems, where parts of the overall solution can be computed independently on parts of the data. The fact that trees can, and should, train on only a subset of features or input data makes it trivial to parallelize building of the trees.

Although Spark MLlib does not yet support it directly, random decision forests can also evaluate their own accuracy along the way, because often trees are built on just a subset of all training data and can be internally cross-validated against the remaining data. This means that the forest can even know which of its trees appear to be the most accurate and weight accordingly.

This property also leads to a way to assess which features of the input are most helpful in predicting the target, and thus help with the problem of feature selection. This is also beyond the scope of this chapter, and MLlib, at the moment.

Making Predictions

Building a classifier, while interesting and a nuanced process, is not the end goal. The goal is to make predictions. This is the payoff, and it is comparatively quite easy. The training set consisted of LabeledPoint instances, each of which contained a Vector and a target value. These are an input and known output, respectively. When we’re making predictions—especially about the future, says Mr. Bohr—the output is of course not known.

The results of the DecisionTree and RandomForest training shown so far are DecisionTreeModel and RandomForestModel objects, respectively. Both contain essentially one method, predict(). It accepts a Vector, just like the feature vector portion of LabeledPoint. So, we can classify a new example by converting it to a feature vector in the same way and predicting its target class:

val input = "2709,125,28,67,23,3224,253,207,61,6094,0,29"
val vector = Vectors.dense(input.split(',').map(_.toDouble))
forest.predict(vector) 

Can also predict for a whole RDD at once

The result should be 4.0, which corresponds to class 5 (the original feature was 1-indexed) in the original Covtype data set. The predicted cover type for the land described in this example is “Aspen.” Obviously.

Where to Go from Here

This chapter introduced two related and important types of machine learning, classification and regression, along with some foundational concepts in building and tuning models: features, vectors, training, and cross-validation. It demonstrated how to predict a type of forest cover from things like location and soil type, using the Covtype data set, with decision trees and forests implemented in Spark MLlib.

As with recommenders in Chapter 3, it could be useful to continue exploring the effect of hyperparameters on accuracy. Most decision tree hyperparameters trade time for accuracy: more bins and trees generally produce better accuracy, but hit a point of diminishing returns.

The classifier here turned out to be very accurate. It’s unusual to achieve more than 95% accuracy. In general, you will achieve further improvements in accuracy by including more features, or transforming existing features into a more predictive form. This is a common, repeated step in iteratively improving a classifier model. For example, for this data set, the two features encoding horizontal and vertical distance to surface water features could produce a third feature: straight-line distance to surface water features. This might turn out to be more useful than either original feature. Or, if it were possible to collect more data, we might try adding new information like soil moisture in order to improve classification.

Of course, not all prediction problems in the real world are exactly like the Covtype data set. For example, some problems require predicting a continuous numeric value, not a categorical value. Much of the same analysis and code applies to this type of regression problem; the trainRegressor() method will be of use in this case instead of trainClassifier().

Furthermore, decision trees and forests are not the only classification or regression algorithms, and not the only ones implemented in Spark MLlib. For classification, it includes implementations of:

• Naïve Bayes

• Support vector machines (SVMs)

• Logistic regression

Yes, logistic regression is a classification technique. Underneath the hood, it classifies by predicting a continuous function of a class probability. This detail is not necessary to understand.

Each of these algorithms operates quite differently from decision trees and forests. However, many elements are the same: they accept an RDD of LabeledPoint as input, and have hyperparameters that you must select using training, cross-validation, and test subsets of the input data. The same general principles, with these other algorithms, can also be deployed to model classification and regression problems.

These have been examples of supervised learning. What happens when some, or all, of the target values are unknown? The following chapter will explore what can be done in this situation.