13.5 Laplace’s Equation

INTRODUCTION

Suppose we wish to find the steady-state temperature u(x, y) in a rectangular plate whose vertical edges x = 0 and x = a are insulated, and whose upper and lower edges y = b and y = 0 are maintained at temperatures f(x) and 0, respectively. See FIGURE 13.5.1. When no heat escapes from the lateral faces of the plate, we solve the following boundary-value problem:

A rectangular plate placed in an x y coordinate plane. The bottom edge of the plate coincides with the x axis and the left edge of the plate coincides with y axis. The top right vertex of the rectangular plate is labeled (a, b). A thin strip to the left and right of the vertical edges of the plate is marked out in barred lines and labeled insulated. The top edge of the plate is indicated by an arrow and labeled u = f(x). The bottom edge is labeled u = 0.

FIGURE 13.5.1 Find the temperature u in a rectangular plate

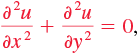(1)

(2)

u(x, 0) = 0, u(x, b) = f(x), 0 < x < a.(3)

Solution of the BVP

With ...

Get Advanced Engineering Mathematics, 7th Edition now with the O’Reilly learning platform.

O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

Start your free trial